
Решение уравнения : ||x - 7| - 2| = 3?
Решение уравнения : ||x - 7| - 2| = 3.
Подробно.

При каких значениях а система неравенств не имеет решений?
При каких значениях а система неравенств не имеет решений?
( Можете пожалуйста ответ объяснить).

Помогите пожалуйста с 3 заданием только с решением пожалуйста?
Помогите пожалуйста с 3 заданием только с решением пожалуйста.

Помогите решить задание 36 под номером 3?
Помогите решить задание 36 под номером 3!
Буду очень благодарна за правильный, подробный ответ!

Помогите решить 5 номер подробно пожалуйста очень нужно?
Помогите решить 5 номер подробно пожалуйста очень нужно.
Заранее спасибо.

100 баллов?
100 баллов.
Желательно, подробно расписать.

Сделайте пожалуйста морфологический разбор местоимения твой( Предложение : Я твой отец) только сделайте подробно пожалуйста, буду очень благодарна?
Сделайте пожалуйста морфологический разбор местоимения твой( Предложение : Я твой отец) только сделайте подробно пожалуйста, буду очень благодарна.

Вот пример, решите его пожалуйста, с решением?
Вот пример, решите его пожалуйста, с решением!
)).

Срочно помогите 368(б, в, г) заранее спасибо?
Срочно помогите 368(б, в, г) заранее спасибо!
Напишите полное решение пожалуйста!
На этой странице находится ответ на вопрос Пожалуйста подробное решение?, из категории Алгебра, соответствующий программе для 10 - 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Алгебра. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

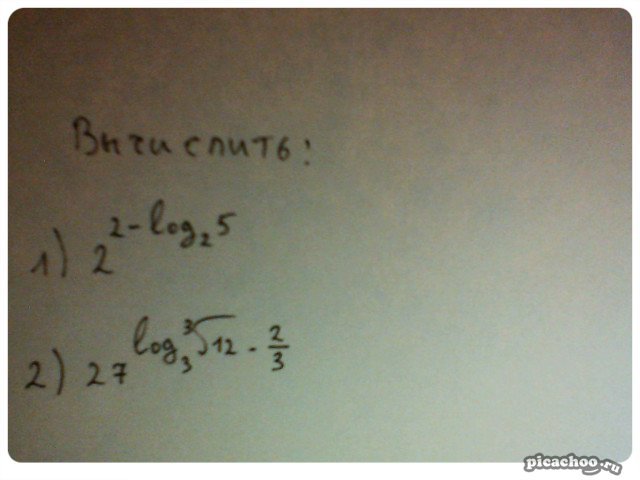
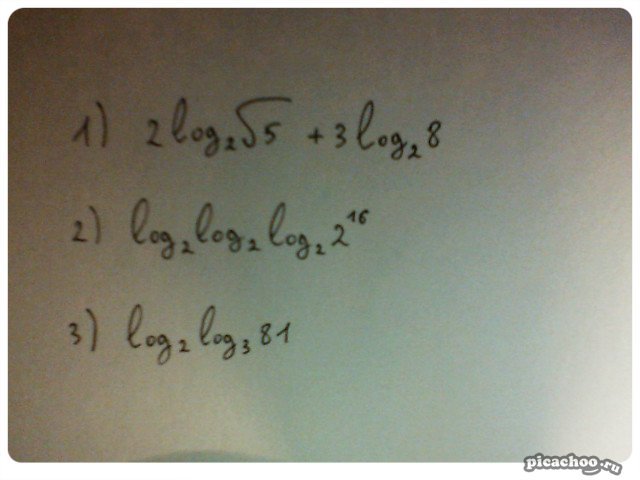



$2^{2-log_25}=2^2\cdot 2^{{log_2}5^{-1}}=4\cdot 5^{-1}=\frac{4}{5}\\\\27^{log_3\sqrt[3]{12}-\frac{2}{3}}=3^{3(log_3(12^{\frac{1}{3}})-\frac{2}{3})}=3^{log_312}\cdot 3^{-2}=12\cdot \frac{1}{9}=\frac{4}{3}\\\\2log_2\sqrt5+3log_28=log_2(\sqrt5)^2+log_2(2^3)^3=log_25+log_22^9=\\\\=log_25+9=\\\\log_2log_2log_22^{16}=log_2log_216=log_2log_22^4=log_24=log_22^2=2$
$log_2log_381=log_2(log_33^4)=log_24=log_22^2=2$.