Решение какого из данных неравенств изображено на рисунке?

Natasha0102030405 21 июн. 2018 г., 05:51:08

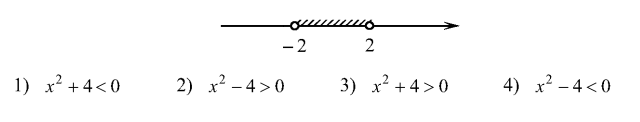
Надо решить каждое неравенство.

1) х ^ 2 + 4< ; 0 x ^ 2 - всегда больше либо равен 0 значит решений нет

2) x ^ 2 - 4> ; 0 x ^ 2> ; 4 / x / > ; 2 при знаке > ; всегда два ответа (если есть модуль х) значит х< ; - 2 x> ; 2 не подходит

3) x ^ 2 + 4> ; 0 x ^ 2> ; - 4 x ^ 2> ; = 0 значит x имеет любое значение

4) остается ответ 4, впрочем он решается аналогично №2 но когда / х / < ; а то х принимает значения : - а< ; x< ; a (где а - какое - то число).

Gorinich368 29 авг. 2018 г., 21:48:01 | 5 - 9 классы

Решить неравенство?

Решить неравенство.

На каком рисунке изображено множество его решений.

Svetulja2010 9 июл. 2018 г., 12:25:52 | 5 - 9 классы

Решение какого из данных неравенств изображено на рисунке?

Решение какого из данных неравенств изображено на рисунке?

И почему?

Bjfyyf 4 февр. 2018 г., 14:52:10 | 5 - 9 классы

На каком рисунке изображено множество решений системы неравенств?

На каком рисунке изображено множество решений системы неравенств.

Natalyaiordek20 12 мар. 2018 г., 23:14:45 | 5 - 9 классы

Решение какого из данных неравенств изображено на рисунке?

Решение какого из данных неравенств изображено на рисунке?

Timoscha1981 15 мая 2018 г., 10:14:08 | 5 - 9 классы

Решение какого из данных неравенств изображено на рисунке?

Решение какого из данных неравенств изображено на рисунке?

АлЁнКо2002 7 янв. 2018 г., 17:29:53 | 5 - 9 классы

Решение какого из данных неравенств изображено на рисунке?

Решение какого из данных неравенств изображено на рисунке?

220379 31 окт. 2018 г., 16:18:15 | 10 - 11 классы

Решение какого из данных неравенств изображено на рисунке?

Решение какого из данных неравенств изображено на рисунке?

Saulesha79 23 апр. 2018 г., 18:10:05 | 5 - 9 классы

На каком рисунке изображено множество решений неравенства?

На каком рисунке изображено множество решений неравенства.

Dashaburova201 12 дек. 2018 г., 15:33:27 | 5 - 9 классы

На каком рисунке изображено множество решений неравенства?

На каком рисунке изображено множество решений неравенства?

Кролчиха 15 июн. 2018 г., 10:22:36 | 5 - 9 классы

#6 и 7?

#6 и 7.

6. Решение какого из данных неравенств изображено на рисунке?

С решением пожалуйста.