Алгебра | 10 - 11 классы
Помогите пожалуйста решить логарифмы, заранее спасибо.
Желательно побыстрее.

Решите, пожалуйста, желательно побыстрее?
Решите, пожалуйста, желательно побыстрее.

Решите логарифм, пожалуйста?
Решите логарифм, пожалуйста!
С решением.
Заранее спасибо!

Логарифмы 400 баллов Помогите пожалуйста с логарифмами Заранее спасибо?
Логарифмы 400 баллов Помогите пожалуйста с логарифмами Заранее спасибо.

Помогите пожалуйста с логарифмами Заранее спасибо?
Помогите пожалуйста с логарифмами Заранее спасибо.

Сделайте пожалуйста очень надо, желательно побыстрее Но заранее большое человеческой спасибо?
Сделайте пожалуйста очень надо, желательно побыстрее Но заранее большое человеческой спасибо!
Извините за качество.

Решить логарифмы, зарание спасибо?
Решить логарифмы, зарание спасибо!

Логарифмы?
Логарифмы!
Хелп!
Фото прилагается Решите примерчик пожалуйста.
Очень срочно!
Желательно как можно подробнее.
Спасибо заранее!
Если нужно, то могу написать пример без фото.

Помогите решить логарифм, заранее спасибо)?
Помогите решить логарифм, заранее спасибо).

Помогите пожалуйста 3 и 4?
Помогите пожалуйста 3 и 4.
Желательно побыстрее.
Заранее Спасибо.

Заранее спасибо решите побыстрее пожалуйста?
Заранее спасибо решите побыстрее пожалуйста.
Вопрос Помогите пожалуйста решить логарифмы, заранее спасибо?, расположенный на этой странице сайта, относится к категории Алгебра и соответствует программе для 10 - 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

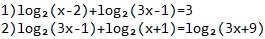


1
ОДЗ
x - 2> ; 0⇒x> ; 2
3x - 1> ; 0⇒x> ; 1 / 3
x∈(2 ; ∞)
log(2)(x - 2)(3x_1) = 3
(x - 2)(3x - 1) = 8
3x² - x - 6x + 2 - 8 = 0
3x² - 7x - 6 = 0
D = 49 + 72 = 121
x1 = (7 - 11) / 6 = - 2 / 3∉ОДЗ
х2 = (7 + 11) / 6 = 3
2
ОДЗ
3x - 1> ; 0⇒x> ; 1 / 3
x + 1> ; 0⇒x> ; - 1
3x + 9> ; 0⇒x> ; - 3
x∈(1 / 3 ; ∞)
log(2)(3x - 1)(x + 1) = log(2)(3x + 9)
(3x - 1)(x + 1) = (3x + 9)
3x² + 3x - x - 1 - 3x - 9 = 0
3x² - x - 10 = 0
D = 1 + 120 = 121
x1 = (1 - 11) / 6 = - 5 / 3∉ОДЗ
х2 = (1 + 11) / 6 = 2.