
B7. Заранее всем спасибо?
B7. Заранее всем спасибо.

Решите производную?
Решите производную.
Заранее спасибо.

Производная?
Производная!
Помогите, пожалуйста, подробно) Заранее большое спасибо!

Помогите пожалуйста найти производную, с решением?
Помогите пожалуйста найти производную, с решением.
Y = - x * lnx * cos2x
заранее спасибо большое!

Помогите пожалуйста запуталась в примере, нужно найти производную f(x) = x ^ 2(x - 1) Заранее спасибо?
Помогите пожалуйста запуталась в примере, нужно найти производную f(x) = x ^ 2(x - 1) Заранее спасибо!

Найдите производную от x ^ arccosx Очень нужна помощь, всем заранее спасибо?
Найдите производную от x ^ arccosx Очень нужна помощь, всем заранее спасибо.

Помогите найти производную?
Помогите найти производную.
Заранее спасибо!
1 / 3 x ^ 3 + 1 / 4x ^ 4 + 2x + 4.

Помогите, пожалуйста, найти производную?
Помогите, пожалуйста, найти производную.
Заранее спасибо)
Задание на фото ниже.

Даю 50 балов распишите подробно для чайника заранее спасибо найти производную кликайте на картинку?
Даю 50 балов распишите подробно для чайника заранее спасибо найти производную кликайте на картинку.

Прошу, помогите найти производную?
Прошу, помогите найти производную.
Спасибо заранее и если можно изложите на листочке внятно и по порядку,.
На этой странице находится ответ на вопрос Помогите найти производную, Заранее спасибо всем = ))?, из категории Алгебра, соответствующий программе для 5 - 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Алгебра. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

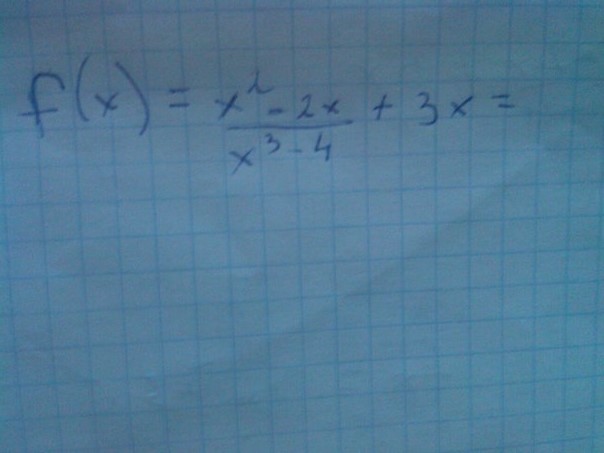



$y'= \frac{(x^2-2x)'*(x^3-4)-(x^2-2x)(x^3-4)'}{(x^3-4)^2}+(3x)'= \frac{(2x-2)*(x^3-4)-3x^2(x^2-2x)}{(x^3-4)^2} +$$3=\frac{-x^4+4x^3-8x+8}{(x^3-4)^2} +3$ = $\frac{-x^4+4x^3-8x+8+3x^6+48-24x^3}{(x^3-4)^2} = \frac{3x^6-x^4-20x^3-8x+56}{(x^3-4)^2}$.