На фото 3 задания ?

Дарья2002love 12 июл. 2018 г., 15:30:59

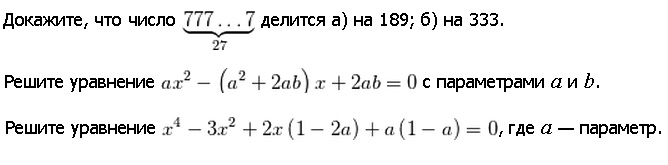
На делимость 189

77777.

(27раз) ее можно переписать ввиде

7 * 111111.

(27 раз) , преобразуем ее к виду

$111....=1*10^{27}+1*10^{26}....1*10^0\\ S_{geom}=\frac{10^{27}-1}{9}$

а так как нужно доказать что она делится на 189, а точнее 189 / 7 = 27 , так как мы уже поделили на 7, тогда нужно теперь доказать что она делится на 27 * 9 = 243

$\frac{10^{27}-1}{243}=\frac{(10-1)(10^2+10+1^2)(10^6+10^3+1)(10^18+10^9+1)}{243}\\ \frac{111(10^6+10^3+1)(10^{18}+10^9+1)}{27}$ так как все числа в знаменателе оканчиваются на 1, то есть они делятся на 3, то оно может представить ввиде$\frac{3^3*x}{2}$ , где х - неизвестное частное, то есть она делится на 27

на делимость 333, вытекает из того что , 111 * 3, так как ранее уже было сказано что любое число содержит в себе множитель 3 , значит тоже делится на 333

2) $ax^2-(a^2+2ab)x+2ab=0\\ D=\sqrt{(a^2+2ab)^2-4a*2ab}$ возможны случаи

$1) D=\sqrt{(a^2+2ab)^2-4a*2ab}=0\\$ тогда корень 1

и он равен $x=\frac{a^2+2ab+\sqrt{(a^2+2ab)^2-8a^2b}}{2a}$

$2) D=\sqrt{(a^2+2ab)^2-4a*2ab}<0$ нет решений

$3) D=\sqrt{(a^2+2ab)^2-4a*2ab}>0\\ x_{1;2}=\frac{a^2+2ab+/-\sqrt{(a^2+2ab)^2-8a^2b}}{2a}$

3)

$x^4-3x^2+2x(1-2a)+a(1-a)=0\\ (x^2-2x-a+1)(x^2+2x+a)=0\\ \left \{ {{x^2-2x-a+1=0} \atop {x^2+2x+a=0}} \right. \\ 1)\\ x^2-2x-(a-1)=0\\ D=\sqrt{4+4(a-1)}=2\sqrt{a}\\ a<0\ net \\ x_{1}=\frac{2+2\sqrt{a}}{2}=1+\sqrt{a}\\ x_{2}=\frac{2-2\sqrt{a}}{2}=1-\sqrt{a}\\ 2)\\ x^2+2x+a=0\\ D=\sqrt{4-4a}=2\sqrt{1-a}\\ 1-a>0\\ x_{3}=\frac{-2+2\sqrt{1-a}}{2}=-1+\sqrt{1-a}\\ x_{4}=\frac{-2-2\sqrt{1-a}}{2}=-1-\sqrt{1-a}$.

Настюня2000 12 февр. 2018 г., 02:17:50 | 5 - 9 классы

ЗАДАНИЕ НА ФОТО, помогите пожалуйста найти наименьшее целое решение неравенства?

ЗАДАНИЕ НА ФОТО, помогите пожалуйста найти наименьшее целое решение неравенства.

Tyrytyty 24 авг. 2018 г., 23:38:41 | 5 - 9 классы

Здраствуйте)помогите пожалуйста с заданием, надо решить уравнение, обязательно с решением задания просто ответы не надо, задание на фото)?

Здраствуйте)помогите пожалуйста с заданием, надо решить уравнение, обязательно с решением задания просто ответы не надо, задание на фото).

Dkozyarskaya 27 мар. 2018 г., 13:35:20 | 5 - 9 классы

Привет?

Привет!

)) на фото задание) спасайте, не понимаю как делать) желательно расписать решение)) спасибо заранее).

Александра287654 8 мар. 2018 г., 07:39:38 | 5 - 9 классы

Нужно быстрое решение любых 3 заданийЖелательно с фото?

Нужно быстрое решение любых 3 заданий

Желательно с фото.

Ddaryaa 18 авг. 2018 г., 07:12:39 | 5 - 9 классы

Задание на фото Прошу написать решение?

Задание на фото Прошу написать решение.

VasilisaDad 29 янв. 2018 г., 07:12:23 | 5 - 9 классы

Помогите решить то , что на фото ?

Помогите решить то , что на фото .

Распишите решение .

Решите задание 19 и 20 .

Kastrovalva 12 мая 2018 г., 08:46:00 | 5 - 9 классы

Распишите подробно решение ?

Распишите подробно решение .

Задание на фото .

Анастасия2093757 8 авг. 2018 г., 03:55:43 | 10 - 11 классы

Пожалуйста помогите , срочно надо?

Пожалуйста помогите , срочно надо.

Можно с подробным решением, а то не понимаю как решать.

Задания на фото.

Мелана 11 сент. 2018 г., 01:38:11 | 10 - 11 классы

Помогите сделать рисунок к решению?

Помогите сделать рисунок к решению.

Фото задания и решений приложено.

Если что то не верно - скажите.

Очень срочно!

Vest550 20 июн. 2018 г., 01:54:46 | 5 - 9 классы

Жду в помощи решению любых заданий с данных фото?

Жду в помощи решению любых заданий с данных фото.