Алгебра | 10 - 11 классы
Даю 35 баллов, решите пожалуйста 9 пример, очень нужно, буду благодарен за помощь!

Даю 15 баллов, решите пожалуйста 143 пример, буду очень благодарен вам за помощь?
Даю 15 баллов, решите пожалуйста 143 пример, буду очень благодарен вам за помощь!

Даю 15 баллов, решите 36 пример пожалуйста, буду очень благодарен за помощь?
Даю 15 баллов, решите 36 пример пожалуйста, буду очень благодарен за помощь!

Даю 15 баллов, решите пожалуйста 16 пример, буду очень благодарен за помощь?
Даю 15 баллов, решите пожалуйста 16 пример, буду очень благодарен за помощь!

Даю 15 баллов, решите пожалуйста 88 пример, буду очень благодарен за помощь?
Даю 15 баллов, решите пожалуйста 88 пример, буду очень благодарен за помощь!

Даю 15 баллов, решите 96 пример пожалуйста, буду очень благодарен вам за помощь?
Даю 15 баллов, решите 96 пример пожалуйста, буду очень благодарен вам за помощь!

Даю 20 баллов, пожалуйста, помогите решить 150 пример, буду очень благодарен вам за помощь?
Даю 20 баллов, пожалуйста, помогите решить 150 пример, буду очень благодарен вам за помощь.

Даю 20 баллов, Решите пожалуйста 121 пример очень нужно, буду очень благодарен?
Даю 20 баллов, Решите пожалуйста 121 пример очень нужно, буду очень благодарен!

Даю 25 баллов, решите пожалуйста 2 пример, очень важно, буду благодарен вам за помощь?
Даю 25 баллов, решите пожалуйста 2 пример, очень важно, буду благодарен вам за помощь.

Даю 20 баллов, решите пожалуйста 1 пример, буду очень благодарен вам за помощь?
Даю 20 баллов, решите пожалуйста 1 пример, буду очень благодарен вам за помощь!

Даю 15 баллов, решите пожалуйста 10 пример, очень нужно, буду благодарен вам за помощь?
Даю 15 баллов, решите пожалуйста 10 пример, очень нужно, буду благодарен вам за помощь!
Вы находитесь на странице вопроса Даю 35 баллов, решите пожалуйста 9 пример, очень нужно, буду благодарен за помощь? из категории Алгебра. Уровень сложности вопроса рассчитан на учащихся 10 - 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

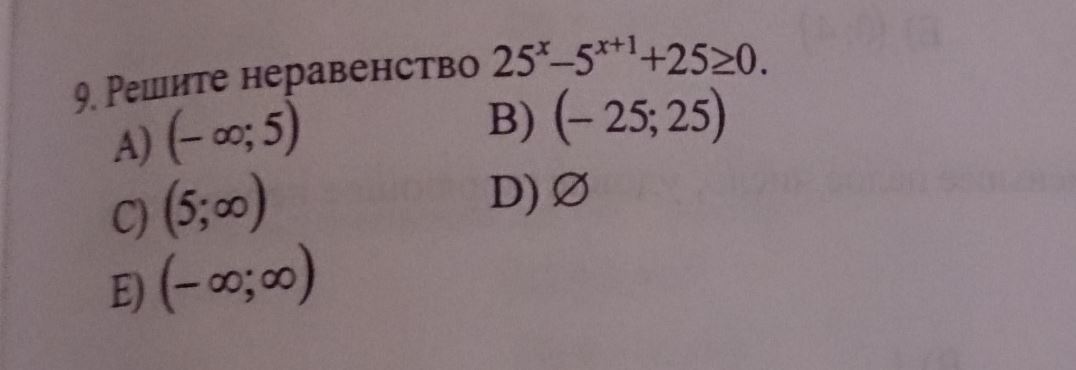




$25^x-5^{x+1}+25 \geq 0\\ (5^x)^2-5^x*5+25 \geq 0\\ 5^x=y\\ y^2-5y+25 \geq 0\\ y^2-5y+25=0\\ D=(-5)^2-4*25=25-100=-75\\ D\ \textless \ 0\\$
Значит ответ будет : х∈ ( - ∞ ; + ∞).