Найти область определения функции с помощью метода интервалов можно пожалуйста решения и объяснения, буду очень благодарен : )?

Danko19 10 мая 2018 г., 15:01:34

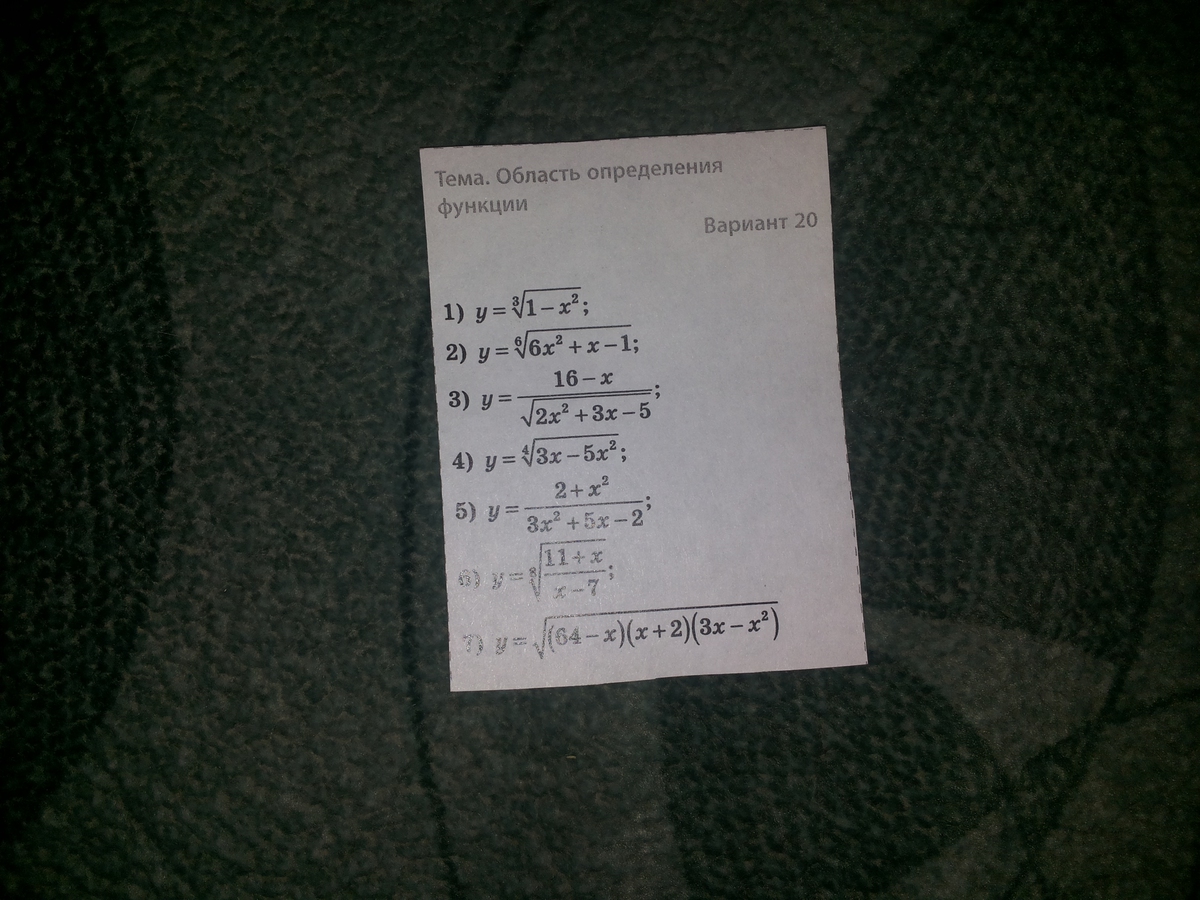
1) D(y) = R или ( - ∞ ; + ∞)

2) 6x² + x - 1≥0 D = 1 + 24 = 25 x₁ = ( - 1 - 5) / 12 = - 6 / 12 = - 1 / 2 x₂ = ( - 1 + 5) / 12 = 4 / 12 = 1 / 3 + - + - - - - - - - - - 1 / 2 - - - - - - - - - - - - 1 / 3 - - - - - - - - - - - - - \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \

D(y) = ( - ∞ ; - 1 / 2]U[1 / 3 ; + ∞)

3) 2x² + 3x - 5> ; 0 D = 9 + 40 = 49 x₁ = ( - 3 - 7) / 4 = - 2.

5 x₂ = ( - 3 + 7) / 4 = 1 + - + - - - - - - - - - 2.

5 - - - - - - - - - - - - 1 - - - - - - - - - - - - - - - \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \

D(y) = ( - ∞ ; - 2.

5)U(1 ; + ∞)

4) 3x - 5x²≥0 5x² - 3x≤0 5x(x - 3 / 5)≤0 x(x - 0.

6)≤0

x = 0 x = 0.

6 + - + - - - - - - - - - - - 0 - - - - - - - - - - - 0.

6 - - - - - - - - - - - - \ \ \ \ \ \ \ \ \ \ \ \ \

D(y) = [0 ; 0.

6]

5) 3x² + 5x - 2≠0 D = 25 + 24 = 49 x₁≠( - 5 - 7) / 6≠ - 2 x₂≠( - 5 + 7) / 6 = 2 / 6≠1 / 3

D(y) = ( - ∞ ; - 2)U( - 2 ; 1 / 3)U(1 / 3 ; + ∞)

6) 1) x - 7≠0 x≠7

2)$\frac{11+x}{x-7} \geq 0$

(11 + x)(x - 7)≥0

(x + 11)(x - 7)≥0

x = - 11 x = 7 + - + - - - - - - - - - 11 - - - - - - - - - - - 7 - - - - - - - - - - - - - \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \

D(y) = ( - ∞ ; - 11]U(7 ; + ∞)

7) (64 - x)(x + 2)(3x - x²)≥0 - (x - 64)(x + 2) * ( - (x² - 3x))≥0 (x - 64)(x + 2)(x² - 3x)≥0 x(x - 64)(x + 2)(x - 3)≥0

x = 0 x = 64 x = - 2 x = 3 + - + - + - - - - - - - - - 2 - - - - - - - - - - 0 - - - - - - - - - 3 - - - - - - - - - - - - 64 - - - - - - - - - - \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \

D(y) = ( - ∞ ; - 2]U[0 ; 3]U[64 ; + ∞).

Nastik055 15 февр. 2018 г., 22:43:10 | 10 - 11 классы

Найти область определения функции?

Найти область определения функции.

Y = Прошу, мне очень срочно : с.

Yamano2013 12 июл. 2018 г., 18:44:10 | 10 - 11 классы

Найти ООФ(область определения функции)у = 3(х - 1) ^ - 2?

Найти ООФ(область определения функции)

у = 3(х - 1) ^ - 2.

С решением пожалуйста).

Us201728 10 апр. 2018 г., 11:20:21 | 10 - 11 классы

Найдите область определения функции буду очень благодарна вам ?

Найдите область определения функции буду очень благодарна вам !

:

Ptanyavamp 8 мая 2018 г., 21:53:22 | 10 - 11 классы

Найти область определения функции?

Найти область определения функции.

Промежутки возрастания и убывания функции.

Помогите, очень надо!

Abdulali 11 окт. 2018 г., 15:53:00 | 5 - 9 классы

Найти область определения функции?

Найти область определения функции.

С подробным решением, пожалуйста.

01aryka 4 нояб. 2018 г., 01:31:51 | 5 - 9 классы

Помогите, пожалуйста найти области определения функций?

Помогите, пожалуйста найти области определения функций!

Yarosh 17 апр. 2018 г., 22:00:15 | 10 - 11 классы

Найдите область определения функции (с объяснением)?

Найдите область определения функции (с объяснением).

Klozina2015 5 июл. 2018 г., 08:43:10 | 10 - 11 классы

Найдите область определения функции ( решением пожалуйста)?

Найдите область определения функции ( решением пожалуйста).

ДЖОРДЖУЗАКОВ 25 дек. 2018 г., 00:00:38 | 10 - 11 классы

Помогите пожалуйста найти области определения функции?

Помогите пожалуйста найти области определения функции.

Sava16232 30 мая 2018 г., 10:48:40 | 10 - 11 классы

Найти область определения функции у = 1 / 2х + 3 с решением, пожалуйста)))?

Найти область определения функции у = 1 / 2х + 3 с решением, пожалуйста))).