Помогите решить систему?

Stydentochka 15 окт. 2018 г., 11:40:01

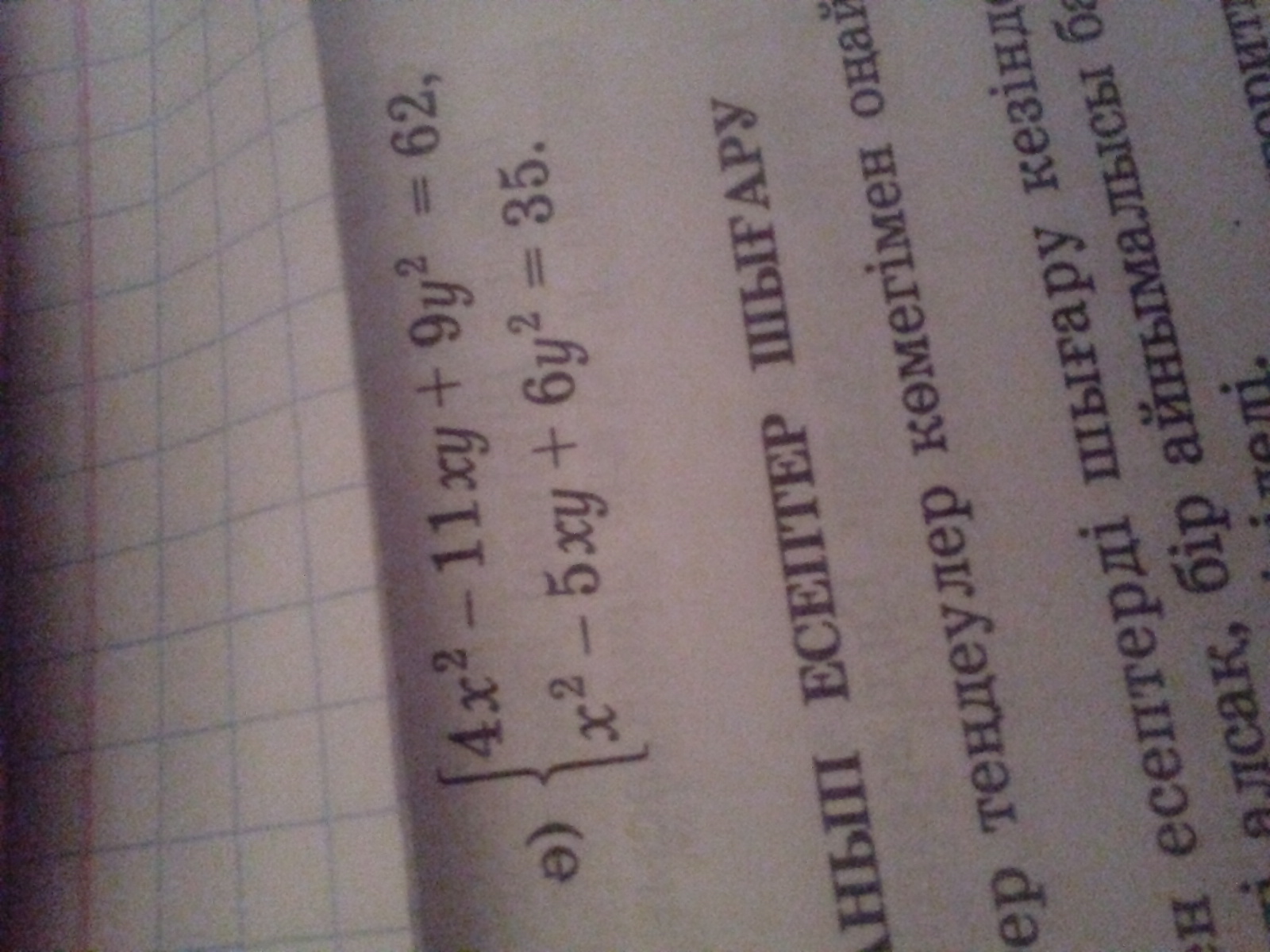
{4x ^ 2 - 11xy + 9y ^ 2 = 62 Вычтим из 1 - ого второе уравнение

{x ^ 2 - 5xy + 6y ^ 2 = 35 ;

{3x ^ 2 - 6xy + 3y ^ 2 = 27 ; x ^ 2 - 2xy + y ^ 2 = 9 ; (x - y) ^ 2 = 3 ; [x - y = - 3 [x - y = 3

Имеем две системы :

1){x - y = - 3 2){x - y = 3 {x ^ 2 - 5xy + 6y ^ 2 = 35 {x * 2 - 5xy + 6y ^ 2 = 35

{x = y - 3

{(y - 3) ^ 2 - 5(y - 3)y + 6y ^ 2 = 35 ; y ^ 2 - 6y + 9 - 5y ^ 2 + 15y + 6y ^ 2 = 35 2y ^ 2 + 9y - 26 = 0 D = 81 - 4 * 2 * ( - 26) = 81 + 208 = 289 = 17 ^ 2 y1 = ( - 9 + 17) / 4 = 8 / 4 = 2 ; y2 = ( - 9 - 17) / 4 = - 13 / 2 = - 6, 5 ;

x1 = 2 - 3 = - 1 ; x2 = - 6, 5 - 3 = - 9, 5 ( - 9, 5 ; - 6, 5) i ( - 1 ; 2) - два решения!

Также решаем вторую систему!

Марина7121 15 окт. 2018 г., 11:40:02

Решение смотри в приложении.

Masha3011 21 мар. 2018 г., 03:51:27 | 5 - 9 классы

Помогите решить систему?

Помогите решить систему!

Suminvas14 4 апр. 2018 г., 08:07:00 | 5 - 9 классы

Помогите?

Помогите.

((не могу решить

Решите систему уравнений методом подстановки : - х - 4у = - 5

2х + 7у = 8 ПОЖАЛУЙСТА !

HarukaGroznaya 22 окт. 2018 г., 17:02:27 | 5 - 9 классы

Помогите решить?

Помогите решить.

Решите систему уравнений.

Bakugan1304 25 окт. 2018 г., 16:23:47 | 10 - 11 классы

Помогите решить систему после выпускного ничего не могу решить аахахах?

Помогите решить систему после выпускного ничего не могу решить аахахах.

Katrinemoore 15 февр. 2018 г., 03:14:16 | 5 - 9 классы

Помогите решить систему?

Помогите решить систему.

Alenkalapka 18 окт. 2018 г., 17:45:47 | 5 - 9 классы

Решите систему уравнений?

Решите систему уравнений.

Помогите пожалуйста, уже надоело, не могу решить.

Помогите с подробным решением.

Пожалуйста!

X + y = 9 y ^ 2 + x = 29.

Umarkadiev451 10 дек. 2018 г., 19:49:49 | 5 - 9 классы

Помогите решить систему?

Помогите решить систему.

Ily12 19 июл. 2018 г., 07:41:17 | 10 - 11 классы

Помогите решить систему ))?

Помогите решить систему )).

Енйетут 13 февр. 2018 г., 08:35:12 | 5 - 9 классы

Помогите решить систему уравнений?

Помогите решить систему уравнений.

3x + 5y = - 9 4x + y = 5 Никак не могу понять, как решить.

Dimavojtsehovsk 25 дек. 2018 г., 16:14:53 | 5 - 9 классы

Помогите решить систему?

Помогите решить систему.