Помогите с пределами?

AZNIX 17 янв. 2022 г., 21:57:48

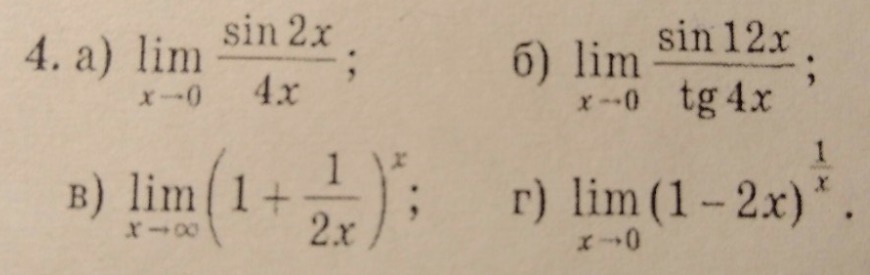
4а) Неопределённость 0 / 0.

Приводим к первому замечательному пределу :

$\lim_{x \to \inft0} \frac{sin2x}{4x} = \frac{1}{2} \lim_{x \to \inft0} \frac{sin2x}{2x}= \frac{1}{2} *1= \frac{1}{2}$

4б) Тоже неопределённость 0 / 0.

Приводим к первому замечательному пределу :

$\lim_{x \to \inft0} \frac{sin12x}{tg4x} =\lim_{x \to \inft0} \frac{sin12x}{ \frac{sin4x}{cos4x} } =\lim_{x \to \inft0} cos4x \frac{sin12x}{ sin4x } = \\ \\ =\lim_{x \to \inft0} cos4x *\lim_{x \to \inft0} \frac{sin12x}{ sin4x } =1*\lim_{x \to \inft0} \frac{sin12x}{ sin4x } = \\ \\ =\lim_{x \to \inft0} \frac{ \frac{sin12x}{x} }{ \frac{sin4x}{x} } = \frac{\lim_{x \to \inft0} \frac{sin12x}{x} } {\lim_{x \to \inft0} \frac{sin4x}{x} } =$

$= \frac{\lim_{x \to \inft0} \frac{12sin12x}{12x} } {\lim_{x \to \inft0} \frac{4sin4x}{4x} } =\frac{12 \lim_{x \to \inft0} \frac{sin12x}{12x} } {4 \lim_{x \to \inft0} \frac{sin4x}{4x} } = \frac{12*1}{4*1} =3$

4в) Неопределённость $1^{\infty}$.

Приводим ко второму замечательному пределу :

$\lim_{x \to \infty} (1+ \frac{1}{2x} )^x=\lim_{x \to \infty} [(1+ \frac{1}{2x} )^{2x* \frac{1}{2x} } ]^x= \\ \\ =\lim_{x \to \infty} [(1+ \frac{1}{2x} )^{2x} ]^{ \frac{1}{2x} *x}=\lim_{x \to \infty} [(1+ \frac{1}{2x} )^{2x} ]^{ \frac{1}{2}}=e^{\frac{1}{2}} = \sqrt{e}$

4г) Неопределённость $1^{\infty}$.

Приводим ко второму замечательному пределу :

$\lim_{x \to \inft0} (1-2x )^{ \frac{1}{x} }=\lim_{x \to \inft0} (1+(-2x) )^{ \frac{1}{x} }= \\ \\ =\lim_{x \to \inft0} [(1+(-2x) )^{ \frac{1}{-2x}* (-2x) } ]^{ \frac{1}{x} }= \\ \\ =\lim_{x \to \inft0} [(1+(-2x) )^{ \frac{1}{-2x}} ]^{ (-2x)* \frac{1}{x} }= \\ \\ =\lim_{x \to \inft0} [(1+(-2x) )^{ \frac{1}{-2x}} ]^{ -2 }=e^{-2}$.

Kuknor200 17 янв. 2022 г., 21:57:54

Task / 26096452 - - - - - - - - - - - - - - - - - - - -

см приложения.

Margo0302 10 янв. 2022 г., 01:02:15 | студенческий

Если функция имеет предел, то только?

Если функция имеет предел, то только.

Prosvirnin 3 янв. 2022 г., 18:56:51 | 10 - 11 классы

Пожалуйста помогите вычислить пределы функций подробно (пожалуйста фото)?

Пожалуйста помогите вычислить пределы функций подробно (пожалуйста фото).

Отличник366 4 янв. 2022 г., 07:04:08 | 10 - 11 классы

Помогите пожалуйста вычислить предел функции в точке?

Помогите пожалуйста вычислить предел функции в точке.

Aeron 6 янв. 2022 г., 08:03:27 | 10 - 11 классы

Пожалуйста помогите вычислить пределы функций на бесконечности?

Пожалуйста помогите вычислить пределы функций на бесконечности.

Galkalova87 30 янв. 2022 г., 21:03:33 | студенческий

Вычислить пределы функций?

Вычислить пределы функций.

Qwemnbp 27 апр. 2022 г., 21:51:51 | студенческий

Помогите вычислить предел?

Помогите вычислить предел.

Lavrovalubov0 26 февр. 2022 г., 01:15:05 | 5 - 9 классы

Вычислите предел на фото?

Вычислите предел на фото.

Aam01 29 апр. 2022 г., 16:35:43 | студенческий

Найти указанный предел?

Найти указанный предел.

Glghgg 23 февр. 2022 г., 23:42:48 | 5 - 9 классы

Помогите с пределом?

Помогите с пределом.

Artlozkin2015Tema 5 июн. 2022 г., 01:56:07 | 5 - 9 классы

Решите пределы, пожалуйста?

Решите пределы, пожалуйста.