Вычислить предел?

Chulpan20021 25 янв. 2022 г., 11:19:54

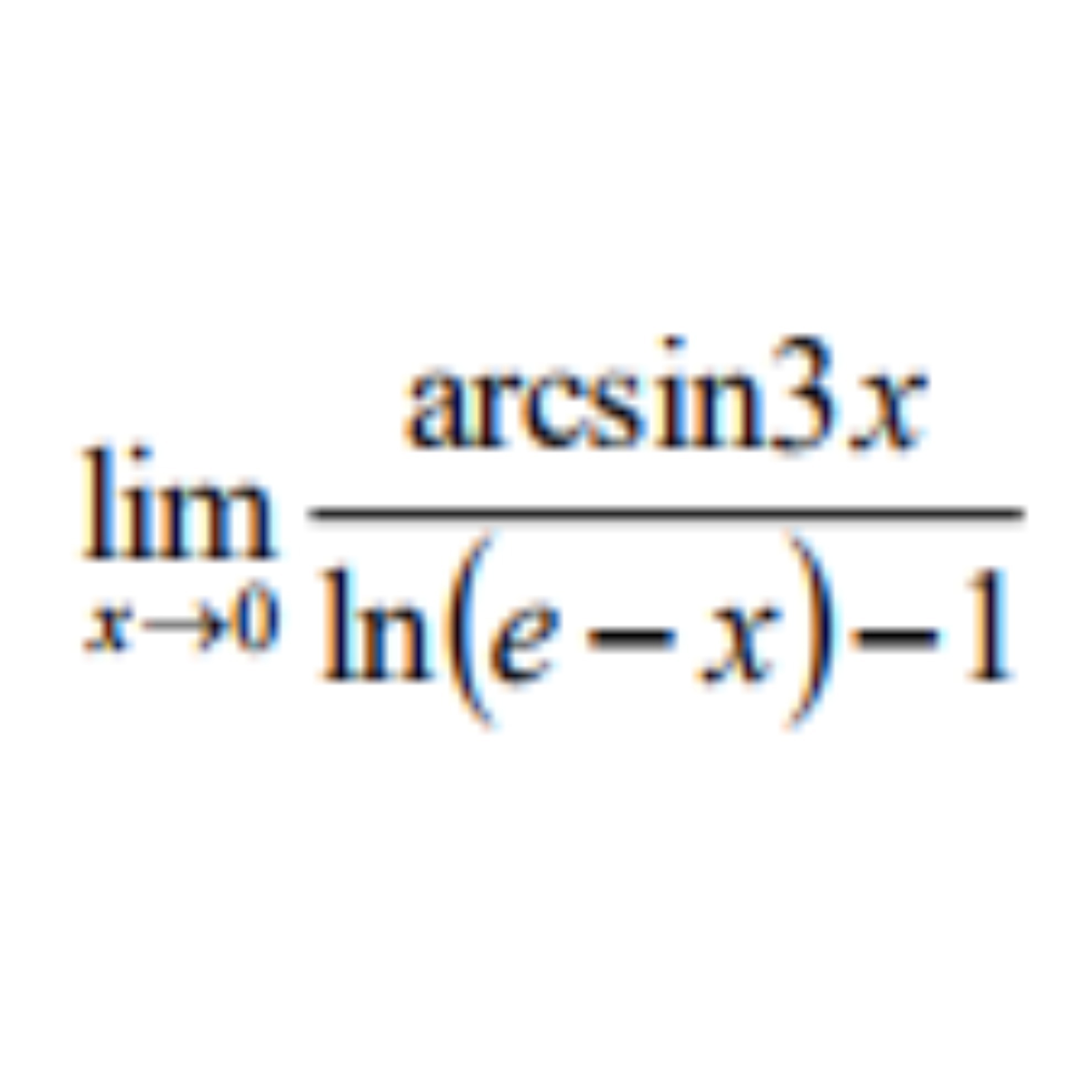
$\lim_{x \to \inft0} \frac{arcsin3x}{ln(e-x)-1}$

Неопределённость 0 / 0.

Разделим числитель и знаменатель на икс (х) :

$\lim_{x \to \inft0} \frac{arcsin3x}{ln(e-x)-1}=\lim_{x \to \inft0} \frac{ \frac{arcsin3x}{x} } { \frac{ln(e-x)-1}{x} }= \frac{\lim_{x \to \inft0} \frac{arcsin3x}{x} }{\lim_{x \to \inft0} \frac{ln(e-x)-1}{x} }$

В числителе чуть - чуть не хватает до первого замечательного предела.

Чтобы это исправить домножим арксинус на 3 и тут же разделим на три :

$\frac{\lim_{x \to \inft0} \frac{3arcsin3x}{3x} }{\lim_{x \to \inft0} \frac{ln(e-x)-1}{x} } =\frac{ 3 \lim_{x \to \inft0} \frac{arcsin3x}{3x} }{\lim_{x \to \inft0} \frac{ln(e-x)-1}{x} }$

Вот теперь в числителе можно применить первый замечательный предел (не в форме синуса, а в форме арксинуса) :

$\frac{ 3 \lim_{x \to \inft0} \frac{arcsin3x}{3x} }{\lim_{x \to \inft0} \frac{ln(e-x)-1}{x} }=\frac{ 3 }{ \lim_{x \to \inft0} \frac{ln(e-x)-1}{x} }$

Теперь обратим внимание на знаменатель - там ещё один предел.

Он приводится ко второму замечательному пределу.

Для простоты будем выполнять действия только со знаменателем :

$\lim_{x \to \inft0} \frac{ln(e-x)-1}{x}=\lim_{x \to \inft0} \frac{ln(e-x)-lne}{x}= \\ \\ =\lim_{x \to \inft0} \frac{ln \frac{e-x}{e} }{x}=\lim_{x \to \inft0} \frac{ln(1- \frac{x}{e} ) }{x}=\lim_{x \to \inft0} \frac{1}{x}ln(1- \frac{x}{e} ) = \\ \\ =\lim_{x \to \inft0} ln(1+ (-\frac{x}{e}) )^{\frac{1}{x}} =\lim_{x \to \inft0} ln[(1+ (-\frac{x}{e}) )^{- \frac{e}{x} *(- \frac{x}{e} )} ]^{\frac{1}{x}} =$

$=\lim_{x \to \inft0} ln[(1+ (-\frac{x}{e}) )^{- \frac{e}{x} } ]^{ (- \frac{x}{e})* \frac{1}{x}} =\lim_{x \to \inft0} ln[(1+ (-\frac{x}{e}) )^{- \frac{e}{x} } ]^{- \frac{1}{e}} = \\ \\ =ln[ \lim_{x \to \inft0} (1+ (-\frac{x}{e}) )^{- \frac{e}{x} } ]^{- \frac{1}{e}} =lne^{- \frac{1}{e}}=- \frac{1}{e}lne=- \frac{1}{e}$

Итак, последовательно подвели знаменатель ко второму замечательному пределу.

Переходим к основному пределу :

$\lim_{x \to \inft0} \frac{arcsin3x}{ln(e-x)-1}=\frac{ 3 }{ \lim_{x \to \inft0} \frac{ln(e-x)-1}{x} }= \frac{3}{- \frac{1}{e}} =-3e$.

Knatusik1983 23 янв. 2022 г., 16:21:29 | 5 - 9 классы

Можете помочь, пожалуйста(x ^ 2 - 9)(2x - 3)?

Можете помочь, пожалуйста

(x ^ 2 - 9)(2x - 3).

Prosvirnin 3 янв. 2022 г., 18:56:51 | 10 - 11 классы

Пожалуйста помогите вычислить пределы функций подробно (пожалуйста фото)?

Пожалуйста помогите вычислить пределы функций подробно (пожалуйста фото).

Отличник366 4 янв. 2022 г., 07:04:08 | 10 - 11 классы

Помогите пожалуйста вычислить предел функции в точке?

Помогите пожалуйста вычислить предел функции в точке.

Aeron 6 янв. 2022 г., 08:03:27 | 10 - 11 классы

Пожалуйста помогите вычислить пределы функций на бесконечности?

Пожалуйста помогите вычислить пределы функций на бесконечности.

Cinare 1 апр. 2022 г., 19:18:28 | 5 - 9 классы

Кроме 5 номера можете помочь?

Кроме 5 номера можете помочь?

YuRET 6 апр. 2022 г., 03:47:20 | студенческий

Можете помочь?

Можете помочь?

Спасибо за ранее.

Galkalova87 30 янв. 2022 г., 21:03:33 | студенческий

Вычислить пределы функций?

Вычислить пределы функций.

Надюшаааа1 17 янв. 2022 г., 02:13:25 | 5 - 9 классы

Можете помочь?

Можете помочь?

Умоляяяяю.

S1u2p3e4r 5 мар. 2022 г., 14:43:52 | 5 - 9 классы

Можете помочь пожалуйста решить примеры?

Можете помочь пожалуйста решить примеры.

Awinerx 9 февр. 2022 г., 03:48:45 | 5 - 9 классы

Помогите пожалуйста ><Новая тема вообще не понятна : СМожете , пожалуйста, помочь?

Помогите пожалуйста ><

Новая тема вообще не понятна : С

Можете , пожалуйста, помочь?

Объяснение не помешает((.