Решите, пожалуйста систему уравнений логарифмическую?

Вомаод 3 янв. 2018 г., 02:35:03

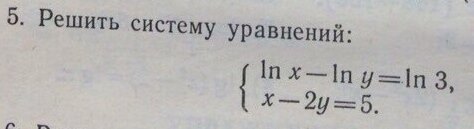
Поскольку главная проблема в навыке решать подобные уравнения, решим аналогичное, чтобы уметь решать любые подобные задачи * * * РЕШИТЬ СИСТЕМУ :

$\ln{2x} - \ln{y} = 3$ ; (I) – первое уравнение системы,

$x + 3y = 18$ ; (II) - второе уравнение системы.

* * * РЕШЕНИЕ :

Первое, область определения уравнения (т.

Е. , когда оно имеет смысл) :

x > ; 0 и y > ; 0 ;

Если выполнены эти условия, то первое уравнение системы можно преобразовать :

$\ln{2x} - \ln{y} = ln{ \frac{2x}{y} }$ ;

При этом, поскольку получается, что $\ln{ \frac{2x}{y} } = \ln{3}$,

значит : $\frac{2x}{y} = 3$ ;

Теперь, просто решим систему подстановкой, выразив x из второго уравнения (II) :

$x = 18 - 3y$ ; (II * ) – следствие из второго уравнения начальной системы.

Подставляем в $\frac{2x}{y} = 3$ и получаем, что $\frac{ 2 ( 18 - 3y ) }{y} = 3$ ;

Домножаем всё на y и получаем, что $2 ( 18 - 3y ) = 3y$ ;

Далее : $36 - 6y = 3y$ ;

[img = 10] ;

[img = 11] ;

Из связи [img = 12] найдйм, что [img = 13] ;

x и y больше нуля, т.

Е. они соответствуют области определения.

* * * ОТВЕТ : ( x ; y ) = ( 6 ; 4 ).

В вашем случае получится такой ответ, что оба числа будут положительными, а в сумме x и y будут давать 20, и оба будут кратными числу 5.

Такая пара чисел – единственна, так что не промахнётесь.

Leha1973 3 янв. 2018 г., 02:35:09

Из первого уравнения :

$lnx - lny = ln3 \\ ln \frac{x}{y} = ln3 \\ \frac{x}{y} =3 \\ x= 3y \\$

Подставим значение Х во второе уравнение :

$x-2y=5 \\ 3y-2y=5 \\ 5y =5 \\ y =1 \\$

тогда

$x= 3y = 3*1 =3 \\$

Ответ : ( 3 ; 1).

Heythem 18 авг. 2018 г., 19:03:05 | 10 - 11 классы

Решите, пожалуйста, Логарифмическое уравнение?

Решите, пожалуйста, Логарифмическое уравнение.

Леcя 4 дек. 2018 г., 12:07:17 | 10 - 11 классы

Решите систему логарифмических неравенств?

Решите систему логарифмических неравенств.

Sokolov250403 19 мая 2018 г., 17:47:35 | 10 - 11 классы

Обьясните, пожалуйста, как решить логарифмической уравнение?

Обьясните, пожалуйста, как решить логарифмической уравнение.

AlexKen 3 авг. 2018 г., 20:04:50 | 5 - 9 классы

Решите логарифмическое уравнение?

Решите логарифмическое уравнение.

Dzonnyya 19 июл. 2018 г., 04:55:04 | 10 - 11 классы

Решите логарифмическое уравнение?

Решите логарифмическое уравнение.

Zabavka 3 июл. 2018 г., 18:41:32 | 10 - 11 классы

Помашите пожалуйста решите логарифмические Уравнения?

Помашите пожалуйста решите логарифмические Уравнения.

Kristino4kaa 13 дек. 2018 г., 04:50:20 | 10 - 11 классы

Решить логарифмическую систему уравнений?

Решить логарифмическую систему уравнений.

Учебавглазпопалаа 24 дек. 2018 г., 15:41:21 | 10 - 11 классы

Решение показательных и логарифмических уравнений и систем?

Решение показательных и логарифмических уравнений и систем.

Помогите решить сколько сможете, пожалуйста.

Регина2112112 1 авг. 2018 г., 23:46:07 | 5 - 9 классы

Решите логарифмическое уравнение ?

Решите логарифмическое уравнение :

Evansroza 8 сент. 2018 г., 03:27:04 | 5 - 9 классы

Решите, пожалуйста, логарифмические уравнения?

Решите, пожалуйста, логарифмические уравнения.

Если можно, то с пояснениями).