Помогите пожалуйста подробно решить неравенства?

Runadin 7 янв. 2018 г., 22:33:16

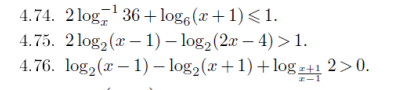
1

ОДЗ

x> ; 0, x≠1, x + 1> ; 0⇒x> ; - 1

x∈(0 ; 1) U (1 ; ∞)

2log ^ - 1(x)36 = log(6)x

log(6)x + log(6)(x + 1)≤1

log(6)(x² + x)≤1

x² + x≤6

x² + x - 6≤0

x1 + x2 = - 1 U x1 * x2 = - 6⇒x1 = - 3 U x2 = 2 - 3≤x≤2 U x∈(0 ; 1) U (1 ; ∞)

Ответ x∈(0 ; 1) U (1 ; 2]

2

ОДЗ

x - 1> ; 0⇒x> ; 1

2x - 4> ; 0⇒x> ; 2

x∈(2 ; ∞)

log(2)[(x - 1)² / (2x - 4)]> ; 1

(x - 1)² / (2x - 4)> ; 2

(x - 1)² / (2x - 4) - 2> ; 0

(x² - 2x + 1 - 4x + 8) / (2x - 4)> ; 0

(x² - 6x + 9) / (2x - 4)> ; 0

(x - 3)² / (2x - 4)> ; 0

x - 3 = 0⇒x = 3

2x - 4 = 0⇒x = 2 _ + + - - - - - - - - - - - - - - (2) - - - - - - - - - - - - - - (3) - - - - - - - - - - - - - - - - - - - -

Ответ x∈(2 ; 3) U (3 ; ∞)

3

ОДЗ

x - 1> ; 0⇒x> ; 1

x + 1> ; 0⇒x> ; - 1

(x + 1) / (x - 1)> ; 0⇒x< ; - 1 U x> ; 1

(x + 1) / (x - 1)≠1⇒x + 1≠x - 1

x∈(1 ; ∞)

log[(x + 1) / (x - 1)]2> ; log(2)(x + 1) - log(2)(x - 1)

log[(x + 1) / (x - 1)]2> ; log(2)[(x + 1) / (x - 1)]

log[(x + 1) / (x - 1)]2> ; 1 / log[(x + 1) / (x - 1)]

log[(x + 1) / (x - 1)]2 = a

a - 1 / a> ; 0

(a² - 1) / a> ; 0

(a - 1)(a + 1) / a> ; 0

a = 1 a = - 1 a = 0 _ + _ + - - - - - - - - - - - - - - - ( - 1) - - - - - - - - - - - (0) - - - - - - - - - - - - - - (1) - - - - - - - - - - - - - 1< ; a< ; 0⇒ - 1< ; log[(x + 1) / (x - 1)]2< ; 0

(x - 1) / (x + 1)< ; 2

(x - 1 - 2x - 2) / (x + 1)< ; 0

(x + 3) / (x + 1)< ; 0⇒ - 3< ; x< ; - 1 не удов усл

a> ; 1⇒log[(x + 1) / (x - 1)]2> ; 1

(x + 1) / (x - 1)< ; 2

(x + 1 - 2x + 2) / (x - 1)< ; 0

(3 - x) / (x - 1)< ; 0

x< ; 1 U x> ; 3 U x> ; 1

Ответ x∈(3 ; ∞).

Lassylawn 8 авг. 2018 г., 01:14:23 | 10 - 11 классы

Помогите решить неравенство, даю 100 баллов)?

Помогите решить неравенство, даю 100 баллов).

Maksabella 7 апр. 2018 г., 12:22:01 | 5 - 9 классы

Помогите пожалуйста подробно решить неравенства?

Помогите пожалуйста подробно решить неравенства.

Даю 20 баллов.

Tuka777 19 мая 2018 г., 23:05:30 | 5 - 9 классы

Помогите пожалуйста подробно решить неравенства?

Помогите пожалуйста подробно решить неравенства.

Даю 18 баллов.

Каст1 14 янв. 2018 г., 12:27:54 | 10 - 11 классы

Нужно решить неравенство?

Нужно решить неравенство.

Пожалуйста подробно с одз ; даю 60 баллов !

Заранее спасибо!

Ustim665 5 янв. 2018 г., 03:41:41 | 10 - 11 классы

Нужно решить неравенство?

Нужно решить неравенство.

Пожалуйста подробно с одз ; даю 70 баллов !

Заранее спасибо!

Violla381 22 мая 2018 г., 04:02:49 | 5 - 9 классы

Помогите пожалуйста нужно решить систему?

Помогите пожалуйста нужно решить систему!

Подробно пожалуйста.

Даю 87 баллов!

Betik2010 13 февр. 2018 г., 06:31:30 | 5 - 9 классы

Здравствуйте, помогите пожалуйста решить неравенство Мне срочно нужно подробное решение с ОДЗ Поэтому даю 99 баллов Надеюсь на вашу помощь, заранее спасибо?

Здравствуйте, помогите пожалуйста решить неравенство Мне срочно нужно подробное решение с ОДЗ Поэтому даю 99 баллов Надеюсь на вашу помощь, заранее спасибо!

Minikotiсkoteik 23 янв. 2018 г., 10:06:29 | 5 - 9 классы

Даю 38 баллов?

Даю 38 баллов!

Решите неравенство (x - 3)(x + 2)> ; 6 Распишите все подробно!

DimezZz 12 авг. 2018 г., 12:27:44 | 5 - 9 классы

ОЧЕНЬ СРОЧНО, ПОМОГИТЕ ПОЖАЛУЙСТА?

ОЧЕНЬ СРОЧНО, ПОМОГИТЕ ПОЖАЛУЙСТА.

ДАЮ 80 БАЛЛОВ!

РЕШИТЕ НЕРАВЕНСТВО.

Кирилл011102 30 июл. 2018 г., 08:43:49 | 10 - 11 классы

Решить две системы уравнений и неравенств очень подробно?

Решить две системы уравнений и неравенств очень подробно.

Даю 40 баллов.