Помогите решить, пожалуйста?

VladShekov 28 июл. 2018 г., 12:17:09

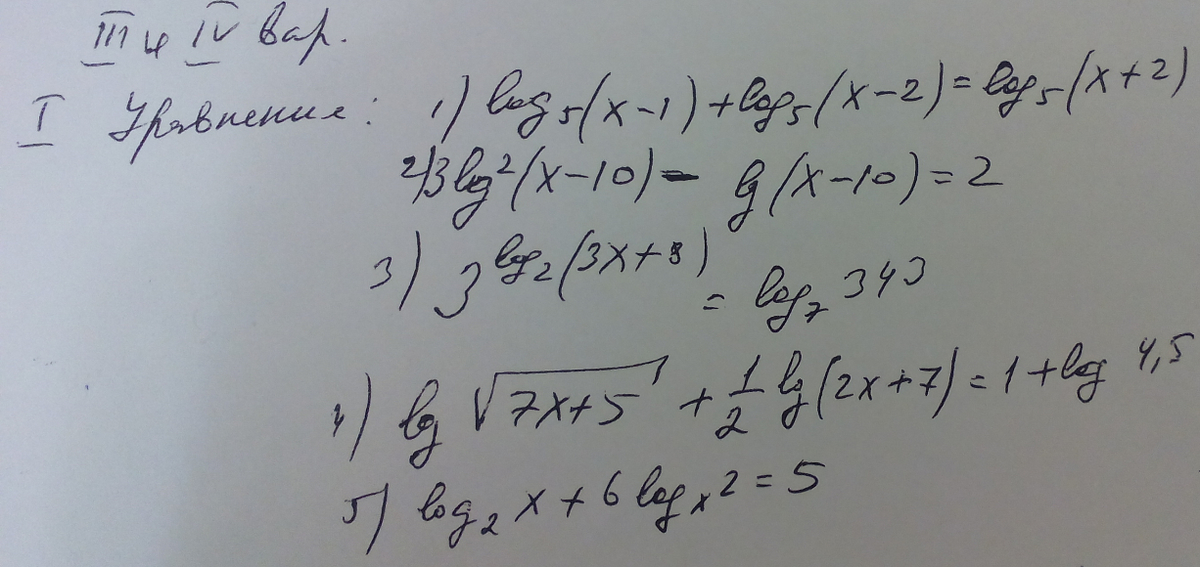
1) В левой части уравнения сумма логарифмом равна логарифму произведения.

По свойству логарифмов :

(х - 1)(х - 2) = х + 2,

х ^ 2 - 3x + 2 - x - 2 = 0,

x ^ 2 - 4x = 0,

x(x - 4) = 0,

х = 0 или х = 4, корень х = 4 удовлетворяет уравнение.

Ответ 4.

2) Сделаем замену : lg(x - 10) = k,

3k ^ 2 - k - 2 = 0,

k1 = 1,

k2 = - 2 / 3.

Произведем обратную замену :

lg(x - 10) = 1,

x - 10 = 10,

x1 = 20.

Lg(x - 10) = - 2 / 3.

X - 10 = 10 ^ ( - 2 / 3).

X - 10 = 1 / ∛100,

x2 = 10 + (1 / ∛100)

Ответ : 20 ; 10 + (1 / ∛100).

3) Сразу отметим, что 343 = 7 ^ 3.

На основании этого можно утверждать, что правая часть уравнения равна 3.

Правая часть уравнения это степень с основанием 3, левая часть уравнения равно 3 в первой степени.

Можем приравнять показатели степеней

log_2(3x + 8) = 3.

3x + 8 = 2 ^ 3,

3x + 8 = 8,

3x = 0,

x = 0.

Ответ : 0.

4) lg√(7x + 5) + 0, 5lg(2x + 7) = 1 + lg4, 5.

Lg10 = 1,

0, 5lg(2x + 7) = lg√(2x + 7).

Уравнение примет вид :

lg√(7x + 5) + lg√(2x + 7) = lg10 + lg4, 5.

Сумму логарифмов превратим в логарифм произведения в каждой части уравнения.

Lg√(7x + 5)(2x + 7) = lg10·4, 5 ;

√(7x + 5)(2x + 7) = 45 ;

Возведем обе части уравнения в квадрат

(7х + 5)(2х + 7) = 2025 ;

Раскроем скобки и приведем подобные

14х ^ 2 + 59x - 1990 = 0 ;

После решения квадратного уравнения получим корень, который удовлетворяет наше уравнение

х = 10.

Ответ : 10.

5) log_2(x) + log_x(2) = 5.

Приведем логарифмы к общему основанию

1 / (log_x(2)) + 6log_x(2) = 5,

Произведем замену

log_x(2) = k,

уравнение примет вид

(1 / k) + 6k = 5,

6k ^ 2 - 5k + 1 = 0.

Решая квадратное уравнение получим два корня :

k1 = 1 / 2 ; k2 = 1 / 3.

Произведем обратную замену

log_x(2) = 1 / 2 ; √x = 2 ; x1 = 4.

Log_x(2) = 1 / 3 ; ∛x = 2 ; x2 = 2 ^ 3 = 8.

Ответ : 4 ; 8.

Elya23 10 июн. 2018 г., 09:33:56 | 10 - 11 классы

Решите пожалуйста?

Решите пожалуйста!

Желательно с подробным решением.

Nara4ka 11 янв. 2018 г., 06:07:33 | 5 - 9 классы

Помогите пожалуйста решить?

Помогите пожалуйста решить.

Желательно подробное решение.

Sashaakarabaeva 31 янв. 2018 г., 11:27:44 | 10 - 11 классы

Помогите пожалуйста решить под буквами Г?

Помогите пожалуйста решить под буквами Г!

Желательно с подробным решением.

Oleg56rus98 15 апр. 2018 г., 18:43:35 | 5 - 9 классы

Помогите решить с очень подробным решением , желательно в формате граффити : *?

Помогите решить с очень подробным решением , желательно в формате граффити : *.

Nastymelnik 1 авг. 2018 г., 01:45:59 | 5 - 9 классы

ПОМОГИ ПОЖАЛУЙСТА желательно с подробным решением?

ПОМОГИ ПОЖАЛУЙСТА желательно с подробным решением.

Dys 25 февр. 2018 г., 10:24:59 | 10 - 11 классы

Помогите, пожалуйста?

Помогите, пожалуйста.

Желательно с подробным решением : ).

Vladimors 20 янв. 2018 г., 21:18:49 | 10 - 11 классы

Помогите, пожалуйста?

Помогите, пожалуйста!

С подробным решением желательно!

Tom7 8 нояб. 2018 г., 19:32:33 | 5 - 9 классы

Помогите пожалуйста, только если не сложно желательно решение с фото и подробным решением?

Помогите пожалуйста, только если не сложно желательно решение с фото и подробным решением.

Veterok2003 25 апр. 2018 г., 00:38:55 | 5 - 9 классы

Помогите решить, пожалуйста?

Помогите решить, пожалуйста.

Желательно, чтоб подробно!

Jandro 17 июл. 2018 г., 20:48:36 | 10 - 11 классы

Помогите пожалуйста?

Помогите пожалуйста.

Желательно с подробным решением.