Найдите натуральное число Х, для которого выполняется равенство (смотрите фото) и объясните весь ход решения - ПОЖАЛУЙСТА?

Arzgir513 24 авг. 2018 г., 06:30:17

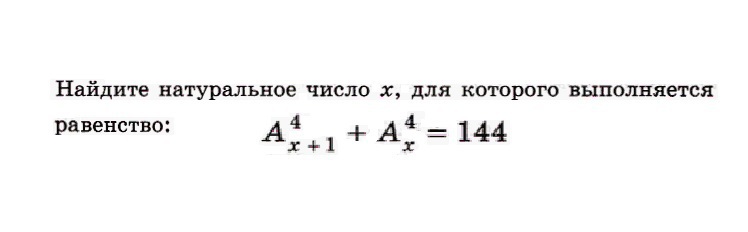
Тут все довольно просто - перестановки вычисляютсяпо формуле :

$A_{m}^{n} = m(m-1)*...* (m-n+1) = \frac{m!}{(m-k)!}$

(Если потребуется вывод - покажу).

Теперь к делу : перебором подберем x.

Пусть x = 4, тогда :

$A_{x+1}^{4} + A_{x}^{4} = A_{5}^{4} + A_{4}^{4} = \frac{5!}{(5-4)!} + \frac{4!}{(4-4)!} =$

Так как 0!

= 1, получим, что :

$=5*4*3*2 + 4*3*2 = (4*3*2)(5+1) = 24*6 = 144$

x = {4} является единственным решением, так как при x = 5

$A_{6}^{4} \ \textgreater \ 144$ ,

что противоречит условию.

Также x не может быть меньше четырех, поскольку это будет противоречить определению формулы перестановок (и здравому смыслу тоже ; ) = > ; x⊂N )

Ответ : x = {4}.

Kbkb2012 24 авг. 2018 г., 06:30:22

Вывести ответ можно так.

Shulia056 19 нояб. 2018 г., 16:58:50 | 10 - 11 классы

Найдите все такие углы a, для каждого из которых выполняется равенство sin a = квадратный корень из 3 / 2 ?

Найдите все такие углы a, для каждого из которых выполняется равенство sin a = квадратный корень из 3 / 2 .

Помогите, пожалуйста!

И если можно объясните, как Вы это сделали.

4946765 9 окт. 2018 г., 10:15:05 | 5 - 9 классы

Найдите 3 различных натуральных числа a, b и c, для которых выполняется равенство ab + bc + ca = abc?

Найдите 3 различных натуральных числа a, b и c, для которых выполняется равенство ab + bc + ca = abc.

Подсказка : разделите обе части равенства на abc.

Shatskova1499 15 июн. 2018 г., 02:46:57 | 5 - 9 классы

Укажите неравенство, решение которого изображено на рисунке (смотрите фото)?

Укажите неравенство, решение которого изображено на рисунке (смотрите фото).

Walldrog 26 апр. 2018 г., 01:18:45 | 5 - 9 классы

Найти натуральное число х, для которого выполняется равенство : Ax ^ 3 - Ax ^ 2 = 0?

Найти натуральное число х, для которого выполняется равенство : Ax ^ 3 - Ax ^ 2 = 0.

Кирило654 30 авг. 2018 г., 10:18:55 | 5 - 9 классы

Подберите такие натуральные числа а и в чтобы выполнялось равенство 3 * а + 6 * в = 1998?

Подберите такие натуральные числа а и в чтобы выполнялось равенство 3 * а + 6 * в = 1998.

CER79 5 нояб. 2018 г., 22:12:06 | 5 - 9 классы

Пожалуйста объясните как решать такие уравнения?

Пожалуйста объясните как решать такие уравнения.

P. S : смотрите фото.

220901sen 28 янв. 2018 г., 01:29:25 | 10 - 11 классы

Объясните пожалуйста ход решения?

Объясните пожалуйста ход решения.

Putinhuilo99 22 мая 2018 г., 16:25:15 | 10 - 11 классы

Решите пример?

Решите пример.

Смотрите на фото.

И можете объяснить решение).

Haталья 27 дек. 2018 г., 07:51:24 | 5 - 9 классы

Фото?

Фото.

Только с ходом решения.

Эльза19 11 мар. 2018 г., 08:27:05 | 1 - 4 классы

Найдите все натуральные значения n, при которых дробь является натуральным числом?

Найдите все натуральные значения n, при которых дробь является натуральным числом.

ФОТО ВНУТРИ.