Алгебра | 10 - 11 классы
Помогите пожалуйста, найдите производную, фото во вложении(желательно подробно распишите).

Помогите сократить дробь (на фото) и подробно распишите как раскладывали квадратное уравнение на множетели?
Помогите сократить дробь (на фото) и подробно распишите как раскладывали квадратное уравнение на множетели.

Помогите, пожалуйста, и распишите подробнее?
Помогите, пожалуйста, и распишите подробнее.

Помогите, пожалуйста, с заданием по алгебре?
Помогите, пожалуйста, с заданием по алгебре!
Задание находится на фото, во вложениях.
Распишите все максимально подробно!
Это важно!
Заранее спасибо!

Распишите подробно решение ?
Распишите подробно решение .
Задание на фото .

Чему равна производная?
Чему равна производная?
Распишите, подробно.

Найти производную?
Найти производную.
Распишите подробно пожалуйста как нашли.

Помогите пожалуйста, распишите подробно?
Помогите пожалуйста, распишите подробно.

Задание на фото решите Распишите подробнее?
Задание на фото решите Распишите подробнее.

Упростите выражение, пжлст, очень подробно распишите, а лучше фото или рисунок?
Упростите выражение, пжлст, очень подробно распишите, а лучше фото или рисунок.

Найдите производную (8x ^ 2) - 16 пожалуйста, распишите подробно?
Найдите производную (8x ^ 2) - 16 пожалуйста, распишите подробно.
Если вам необходимо получить ответ на вопрос Помогите пожалуйста, найдите производную, фото во вложении(желательно подробно распишите)?, относящийся к уровню подготовки учащихся 10 - 11 классов, вы открыли нужную страницу. В категории Алгебра вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

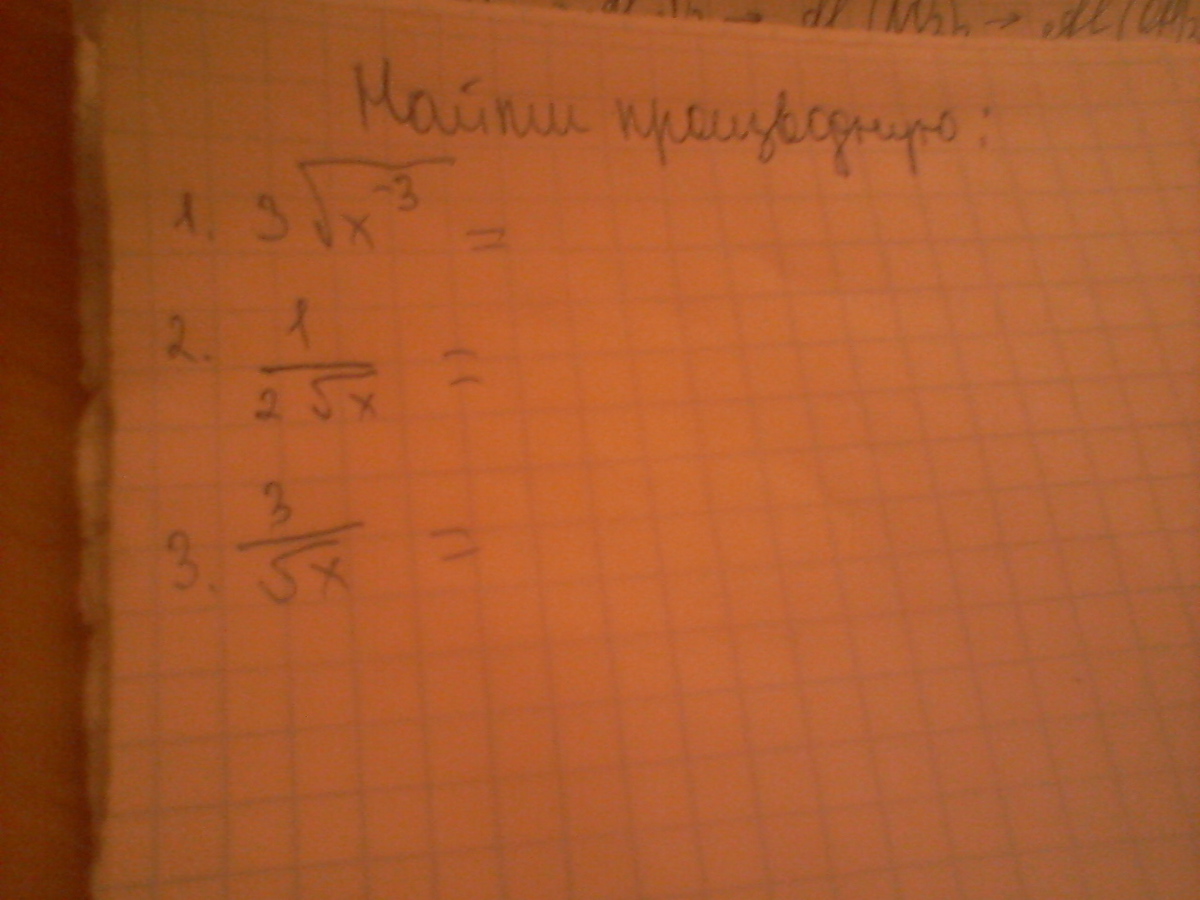




$(3 \sqrt{x^{-3}})'=(3x^{-\frac{3}{2}})'=3*(-\frac{3}{2})x^{-\frac{3}{2}-1}=-\frac{9}{2}x^{-\frac{5}{2}}=-4.5 \sqrt{x^{-5}} \\ (\frac{1}{2\sqrt{x}})'=(\frac{1}{2} \frac{1}{x^{\frac{1}{2}}})'=(\frac{1}{2}x^{-\frac{1}{2}}})'=\frac{1}{2}*(-\frac{1}{2})x^{-\frac{1}{2}-1}=-\frac{1}{4}x^{-\frac{3}{2}}=-\frac{1}{4} \frac{1}{x^{\frac{3}{2}}}= \\ =-\frac{1}{4} \frac{1}{ \sqrt{x^3}}=- \frac{1}{4 \sqrt{x^3}}$
$(\frac{3}{ \sqrt{x}})'=(\frac{3}{x^{ \frac{1}{2}}})'=(3*x^{- \frac{1}{2}})'=3*(- \frac{1}{2})x^{-\frac{1}{2}-1}=- \frac{3}{2}x^{- \frac{3}{2}}=-\frac{3}{2}\frac{1}{x^{\frac{3}{2}}}= \\ =-\frac{3}{2} \frac{1}{ \sqrt{x^3}}=-\frac{3}{2 \sqrt{x^3}}$.