В первом задании нужно найти Область Определения Функции?

Katrina008 30 янв. 2018 г., 02:53:38

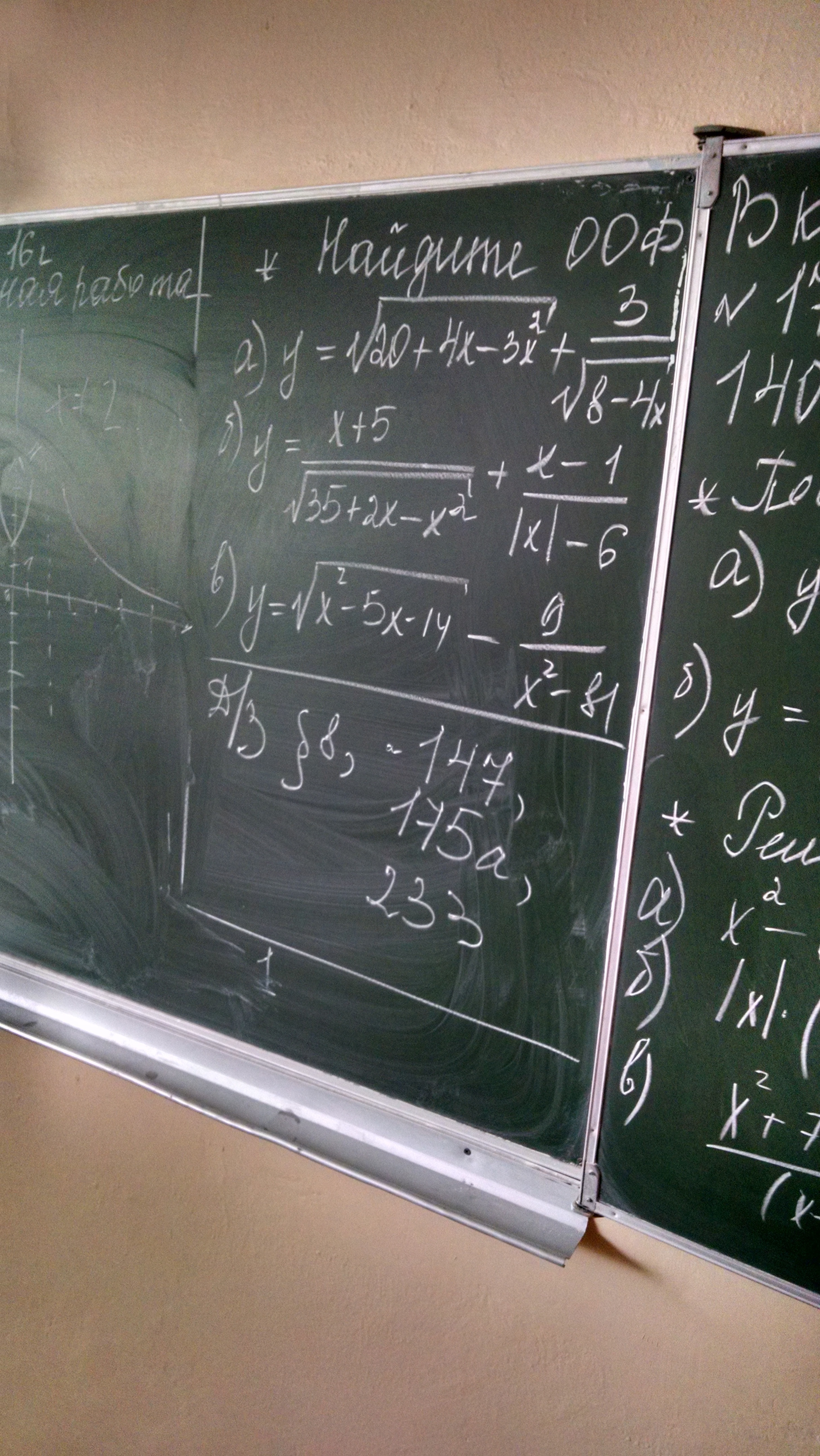
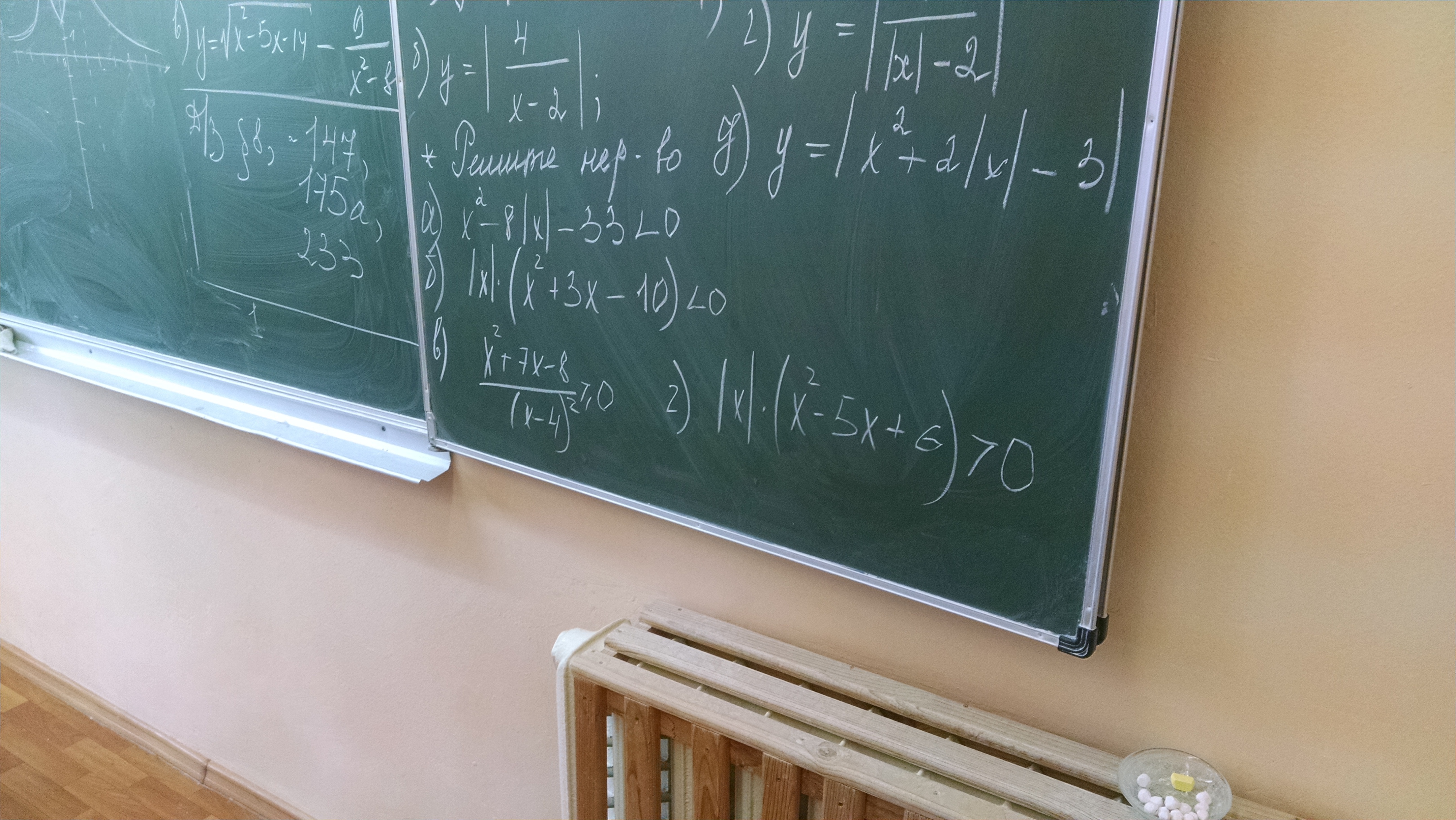
Найти ООФ

а){20 + 4x - 3x²≥0⇒3x² - 4x - 20≤0

D = 16 + 240 = 256 x1 = (4 - 16) / 6 = - 2 U x2 = (4 + 16) / 6 = 10 / 3 - 2≤x≤10 / 3

{8 - 4x> ; 0⇒4x< ; 8⇒x< ; 2

x∈[ - 2 ; 2)

б){35 + 2x - x²≥0⇒x² - 2x - 35≤0 x1 + x2 = 2 U x1 * x2 = - 35 x1 = 7 U x2 = 5⇒ - 5≤x≤7

{|x| - 6≠0⇒|x|≠6⇒x≠ - 6 U x≠6

x∈[ - 5 ; 6) U (6 ; 7]

в){x² - 5x - 14≥0 x1 + x2 = 5 U x1 * x2 = - 14 x1 = - 2 U x2 = 7⇒ x≤ - 2 U x≥7

{x² - 81≠0⇒x²≠81⇒x≠ - 9 U x≠9

x∈( - ∞ ; - 9) U ( - 9 ; - 2] U [7 ; 9) U (9 ; ∞)

Решить неравенство

а)x² - 8|x| - 33< ; 0

1)x< ; 0

x² + 8x - 33< ; 0

x1 + x2 = - 8 U x1 * x2 = - 33⇒x1 = - 11 U x2 = 3 - 11< ; x< ; 3

x∈( - 11 ; 0)

2)x≥0

x² - 8x - 33< ; 0

x1 + x2 = 8 U x1 + x2 = - 33⇒x1 = - 3 U x2 = 11 - 3< ; x< ; 11

x∈[0 ; 11)

Ответ x∈( - 11 ; 11)

б)|x| * (x² + 3x - 10)< ; 0

1)x< ; 0

x(x² + 3x - 10)> ; 0

x = 0

x1 + x2 = - 3 U x1 * x2 = - 10⇒x = - 5 U x2 = 2 _ + _ + - - - - - - - - - - - - - ( - 5) - - - - - - - - - - - (0) - - - - - - - - - - - - - - - - (2) - - - - - - - - - - - -

x∈( - 5 ; 0)

2)x> ; 0

x(x² + 3x - 10)< ; 0

x = 0

x1 + x2 = - 3 U x1 * x2 = - 10⇒x = - 5 U x2 = 2 _ + _ + - - - - - - - - - - - - - ( - 5) - - - - - - - - - - - (0) - - - - - - - - - - - - - - - - (2) - - - - - - - - - - - -

x∈(0 ; 2)

Ответ x∈( - 5 ; 0) U (0 ; 2)

в)(x² + 7x - 8) / (x - 4)²≥0

x² + 7x - 8 = 0

x1 + x2 = - 7 U x1 * x2 = - 8

x1 = - 8 U x2 = 1

x - 4 = 0⇒x = 4 + _ + + - - - - - - - - - - - - - - - - [ - 8] - - - - - - - - - - - [1] - - - - - - - - - - - - - - - - - - - (4) - - - - - - - - - - - - - - - - -

x∈( - ∞ ; - 8] U [1 ; 4) U (4 ; ∞)

г)|x| * (x² - 5x + 6)> ; 0

1)x< ; 0

x * (x² - 5x + 6)< ; 0

x = 0

x1 + x2 = 5 U x1 * x2 = 6⇒x1 = 2 U x2 = 3 _ + _ + - - - - - - - - - - - - - - (0) - - - - - - - - - - - - - - - - (2) - - - - - - - - - - - - - - (3) - - - - - - - - - - - - - -

x∈( - ∞ ; 0)

2)x> ; 0

x * (x² - 5x + 6)> ; 0

x∈(0 ; 2) U (3 ; ∞)

Ответ x∈( - ∞ ; 0) U (0 ; 2) U (3 ; ∞).

Svetlanakuzmin2 12 дек. 2018 г., 19:58:52 | 10 - 11 классы

Алгебра?

Алгебра.

Найти область определения функции.

Фото во вложении.

Под а и б, заранее спасибо.

Yakudza226 12 февр. 2018 г., 08:49:44 | 5 - 9 классы

Найдите область определения функции, только В) заранее спасибо)?

Найдите область определения функции, только В) заранее спасибо).

Katyafilina1 15 мая 2018 г., 21:37:22 | 5 - 9 классы

ПЛИЗ?

ПЛИЗ.

НИКАК НЕ МОГУ СДЕЛАТЬ ПРАВИЛЬНО.

НЕ ПОЛУЧАЕТСЯ.

НАЙДИТЕ ТОЛЬКО ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ.

(ЗАДАНИЕ НА ФОТО.

) ЗАРАНЕЕ СПАСИБО.

Emuaa05 14 мая 2018 г., 15:53:11 | 10 - 11 классы

Найдите область определения функции ПОЖАЛУЙСТА?

Найдите область определения функции ПОЖАЛУЙСТА!

)

Пожалуйста, СРОЧНО, одно из заданий контрольной работы!

) Заранее спасибо!

).

Zahartova 26 мая 2018 г., 01:52:45 | 10 - 11 классы

ПОМОГИТЕ СРОЧНО?

ПОМОГИТЕ СРОЧНО!

Найти область определения функции.

Спасибо : 3.

Irina9816 19 дек. 2018 г., 21:25:36 | 10 - 11 классы

1) Найдите область определения функции 2) Решите неравенство?

1) Найдите область определения функции 2) Решите неравенство.

AnnaKyzina 12 авг. 2018 г., 09:33:20 | 10 - 11 классы

Помогите решить срочно , нужно найти область определения функции?

Помогите решить срочно , нужно найти область определения функции.

Regiromanova9 28 нояб. 2018 г., 09:25:49 | 10 - 11 классы

Нужно найти область определения функций?

Нужно найти область определения функций.

Sovushka5 11 нояб. 2018 г., 00:54:14 | 5 - 9 классы

ДАЮ 99 баллов?

ДАЮ 99 баллов!

Решите задание 1.

5! Надо найти область определения функции.

Khamirzovaru 18 июн. 2018 г., 20:50:13 | 10 - 11 классы

Помогите выполнить задание : Найти область определения функции?

Помогите выполнить задание : Найти область определения функции.