Решить иррациональное неравенство?

Directioner0 19 дек. 2018 г., 03:41:50

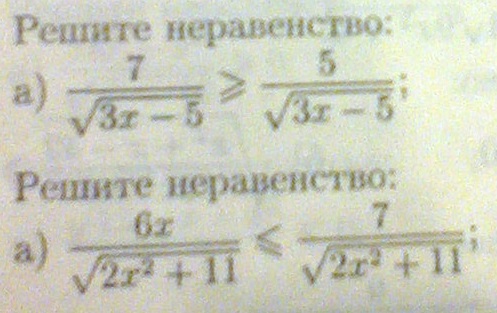
А)$\displaystyle \frac7{\sqrt{3x-5}} \ge \frac5{\sqrt{3x-5}}$$\displaystyle \sqrt{3x-5} >0$ как корень в знаменателе, поэтому при сокращении на это выражение знак неравенства сохранится, но надо помнить об условии существовании этого выражения.

$\displaystyle \begin{Bmatrix}7\ge 5\quad \rightarrow x\in \mathbb{R}\\ 3x-5\ge 0\qquad \quad \\3x-5\ne 0 \qquad \quad \end{matrix} ;\\ \\3x-5>0\\ x>\frac53$Ответ : $\displaystyle x\in \bigg( \frac53 ;\infty \bigg) .$б)$\displaystyle \frac{6x}{\sqrt{2x^2+11}} \le \frac7{\sqrt{2x^2+11}}$Сократим аналогично предыдущему пункту.

Сокращаем мы потому, что выражения абсолютно одинаковы и не влияют на знак неравенства.

$\displaystyle \begin{Bmatrix}6x\le 7\quad \\ 2x^2+11\ge 0\\2x^2+11\ne 0\end{matrix} ;\\ \\ \begin{Bmatrix}x\le \frac76\quad \quad\\ 2x^2>-11\quad \rightarrow x\in \mathbb{R}\end{matrix} \\ x\le \frac76$Ответ : $\displaystyle x\in \bigg( -\infty ;\frac76\bigg) .$.

Jfhnxbzdbdf 16 сент. 2018 г., 20:26:11 | 10 - 11 классы

Иррациональные неравенства?

Иррациональные неравенства.

7Камилла7 5 сент. 2018 г., 02:21:35 | 10 - 11 классы

Решите иррациональное неравенство : корень из икс больше или равно 2?

Решите иррациональное неравенство : корень из икс больше или равно 2.

Nilo1234459 25 мар. 2018 г., 18:45:14 | 5 - 9 классы

Решить иррациональное неравенство?

Решить иррациональное неравенство.

Колесникова1973 16 авг. 2018 г., 07:11:52 | 10 - 11 классы

Иррациональные неравенства?

Иррациональные неравенства.

Kremer 28 февр. 2018 г., 19:40:17 | 5 - 9 классы

Решите иррациональное неравенство?

Решите иррациональное неравенство.

Simbioz111 28 авг. 2018 г., 19:01:09 | 10 - 11 классы

Решить иррациональное уравнение и неравенство?

Решить иррациональное уравнение и неравенство.

Спасибо.

Nekitckyp 29 дек. 2018 г., 07:38:09 | 10 - 11 классы

Решить иррациональное неравенство корень из x + 8> ; x + 2?

Решить иррациональное неравенство корень из x + 8> ; x + 2.

Мирммиирспр 13 апр. 2018 г., 15:30:45 | 10 - 11 классы

Решите иррациональное неравенство?

Решите иррациональное неравенство.

Elia67 22 мая 2018 г., 01:05:56 | 5 - 9 классы

Решите иррациональное неравенство?

Решите иррациональное неравенство.

Ушаковаэрика 27 июл. 2018 г., 03:56:28 | 10 - 11 классы

Помогите решить "Иррациональные уравнения и неравенства"?

Помогите решить "Иррациональные уравнения и неравенства".