Помогите решить домашнее задание с логарифмами?

Mira1804 24 дек. 2018 г., 04:32:28

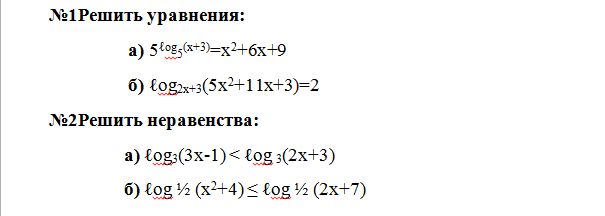
1)ОДЗ : x + 3> ; 0 x> ; - 3

$5^{log_5(x+3)}=x^2+6x+9\\x+3=x^2+6x+9\\x^2+5x+6=0\\D=25-24=1\\x_1=\frac{-5+1}{2}=-2\\x_2=\frac{-5-1}{2}=-3$ - 3 неуд.

ОДЗ. Ответ : х = - 2

2)ОДЗ : 2x + 3> ; 0 $2x+3\neq1$ x> ; - 1.

5 $x\neq-1$

$log_{2x+3}(5x^2+11x+3)=2 \\5x^2+11x+3=(2x+3)^2\\5x^2+11x+3=4x^2+12x+9\\x^2-x-6=0\\D=1+24=25\\x_1=\frac{1+5}{2}=3\\x_2=\frac{1-5}{2}=-2$ - 2 неуд.

ОДЗ. Ответ : х = 3

1)ОДЗ : 3x - 1> ; 0 x> ; 1 / 3

$log_3(3x-1)

Включаея ОДЗ :

$\boxed{x\in (\frac{1}{3};4)}$

2)ОДЗ : 2x + 7> ; 0 x> ; - 3.

5

$log_\frac{1}{2}(x^2+4)\leq log_\frac{1}{2}(2x+7)\ \ \ \ \ \ \ \ \ \ 0<\frac{1}{2}<1\\x^2+4\geq2x+7\\x^2-2x-3\geq0\\(x-3)(x+1)\geq0\\\ x\in (-\infty;-1]\cup[3;+\infty)$

Включая ОДЗ :

$\boxed{(-3.5;-1]\cup[3;+\infty)}$.

Wrestlingmanija001 19 янв. 2018 г., 07:34:13 | 10 - 11 классы

Помогите решить 2 и 4 задание по логарифмам?

Помогите решить 2 и 4 задание по логарифмам.

1рлтодд 13 июл. 2018 г., 05:06:37 | 5 - 9 классы

Помогите с логарифмами, задание вложено?

Помогите с логарифмами, задание вложено.

Lediliana 31 июл. 2018 г., 17:52:35 | 10 - 11 классы

Логарифмы?

Логарифмы.

Помогите решить, фотография в задании.

Найти :

Asadzade2015 22 февр. 2018 г., 07:28:56 | 5 - 9 классы

Логарифмы Помогите с любым из заданий, пожалуйста?

Логарифмы Помогите с любым из заданий, пожалуйста.

Миланапономаренко12 24 апр. 2018 г., 19:34:10 | 10 - 11 классы

Задания с логарифмами, помогите решить все?

Задания с логарифмами, помогите решить все.

Кроме 1 - го.

Что - то не складывается у меня с решением.

Ksen4ik2001 22 мар. 2018 г., 15:39:33 | 5 - 9 классы

Помогите решить домашние задание)?

Помогите решить домашние задание).

Wycc1000 1 мая 2018 г., 17:18:41 | 10 - 11 классы

Ребят помогите ЛОГАРИФМЫ?

Ребят помогите ЛОГАРИФМЫ.

Свойства логарифмов.

Задание А3, В1, В2.

Anarnakhmetov45 15 июн. 2018 г., 18:16:08 | 5 - 9 классы

Помогите решить домашнее задание плиииз?

Помогите решить домашнее задание плиииз.

Shkolniца 28 дек. 2018 г., 22:41:39 | 5 - 9 классы

Помогите с заданием с логарифмами, пожалуйстазадание внутри?

Помогите с заданием с логарифмами, пожалуйста

задание внутри!

Akimiwa9322 26 апр. 2018 г., 09:40:25 | 5 - 9 классы

Помогите решить логарифм?

Помогите решить логарифм.