100 БАЛЛОВ?

Adiloar 6 окт. 2018 г., 14:34:35

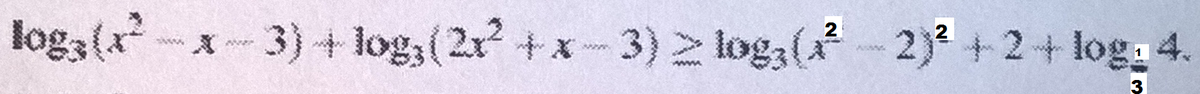
$log_3(x^2-x-3)+log_3(2x^2+x-3) \geq log_3(x^2-2)^2+2+log_{\frac{1}{3}}4\\\\ODZ:\; \left \{ {{x^2-x-3\ \textgreater \ 0} \atop {2x^2+x-3\ \textgreater \ 0}} \right. \; \left \{ {{x\in (-\infty ,\frac{1-\sqrt{13}}{2})\cup (\frac{1+\sqrt{13}}{2},+\infty )} \atop {x\in (-\infty ,-\frac{3}{2})\cup (1,+\infty )}} \right. \to \\\\x\in (-\infty ,-\frac{3}{2})\cup (\frac{1+\sqrt{13}}{2},+\infty )$

$2=log_33^2=log_39; log_{\frac{1}{3}}4=-log_34\; ,\; \; \to \\\\log_3\left (((x^2-x-3)(2x^2+x-3)\right )-log_3\frac{9(x^2-2)^2}{4} \geq 0$

Mетод рационализации :

$(3-1)\cdot ((x^2-x-3)(2x^2+x-3)-\frac{9\cdot (x^2-2)^2}{4}) \geq 0\\\\2x^4-x^3-10x^2+9-\frac{9}{4}x^4+9x^2-9 \geq 0\\\\-\frac{1}{4}x^4-x^3-x^2 \geq 0\\\\-x^2(\frac{1}{4}x^2+x+1) \geq 0\\\\x^2(x^2+4x+4) \leq 0\\\\x^2(x+2)^2 \leq 0\; \; \to \; \; x=0\notin ODZ,\; \; x=-2\in ODZ\\\\Otvet:\; x=-2.\\\\--$.

Nastenaseva 6 окт. 2018 г., 14:34:40

$log0,5(2x-3)\ \textgreater \ log0,3(x2-6)$.

Elya23 10 июн. 2018 г., 09:33:56 | 10 - 11 классы

Решите пожалуйста?

Решите пожалуйста!

Желательно с подробным решением.

Paaappp 4 нояб. 2018 г., 11:33:00 | 5 - 9 классы

Решите неравенство, с решением подробным?

Решите неравенство, с решением подробным.

Sdrgeg 29 июн. 2018 г., 16:40:02 | 10 - 11 классы

Почему этот логарифм равен 2, 5?

Почему этот логарифм равен 2, 5?

Желательно подробнее.

Comedozzz 5 мар. 2018 г., 17:10:52 | 10 - 11 классы

Задание с логарифмами (на картинке внутри)?

Задание с логарифмами (на картинке внутри).

Желательно подробное решение.

80 баллов.

Kbangen 14 дек. 2018 г., 06:39:36 | 10 - 11 классы

Помогите решить логарифмы?

Помогите решить логарифмы.

Нужно подробно как - то расписать в решении что и откуда.

Oksananaumova1 6 мая 2018 г., 11:33:12 | 10 - 11 классы

100 БАЛЛОВ?

100 БАЛЛОВ!

СРОЧНО!

Решите неравенство с логарифмами!

Желательно с подробным решением!

Эбрик 22 мая 2018 г., 18:48:45 | 10 - 11 классы

Решите неравенство?

Решите неравенство.

Подробное решение.

РенатаКосмос 15 нояб. 2018 г., 03:37:38 | 10 - 11 классы

100 БАЛЛОВ?

100 БАЛЛОВ!

Решите неравенство с логарифмами!

Желательно с подробным решением!

Teisole 27 янв. 2018 г., 15:21:19 | 10 - 11 классы

Решите неравенство, желательно по подробнее?

Решите неравенство, желательно по подробнее.

Oksa7878 25 янв. 2018 г., 20:37:09 | 10 - 11 классы

ДАЮ 100 БАЛЛОВ?

ДАЮ 100 БАЛЛОВ.

ПОМОГИТЕ С ЛОГАРИФМАМИ !

ПОДРОБНОЕ РЕШЕНИЕ.