Решите, пожалуйста Вычислить значение выражения : Картинка прилагается?

Pelageya001 16 нояб. 2018 г., 02:35:58

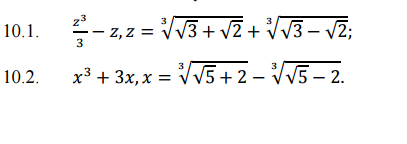
$z=\sqrt[3]{\sqrt3+\sqrt2}+\sqrt[3]{\sqrt3-\sqrt2}\\\\(a+b)^3=a^3+3a^2b+3ab^2+b^3=a^3+b^3+3ab(a+b)\\\\z^3=(\sqrt3+\sqrt2)+(\sqrt3-\sqrt2)+3\sqrt[3]{(\sqrt3+\sqrt2)(\sqrt3-\sqrt2)}\cdot \\\\\cdot (\sqrt[3]{\sqrt3+\sqrt2}+\sqrt[3]{\sqrt3-\sqrt2})=2\sqrt3+3\sqrt[3]{3-2}\cdot \\\\\cdot (\sqrt[3]{\sqrt3+\sqrt2}+\sqrt[3]{\sqrt3-\sqrt2})=2\sqrt3+3(\sqrt[3]{\sqrt3+\sqrt2}+\sqrt[3]{\sqrt3-\sqrt2})\\\\\frac{z^3}{3}-z=\frac{z^3-3z}{3}=$

$=\frac{2\sqrt3+3(\sqrt[3]{\sqrt3+\sqrt2}+\sqrt[3]{\sqrt3-\sqrt2})-3(\sqrt[3]{\sqrt3+\sqrt2}+\sqrt[3]{\sqrt3-\sqrt2})}{3}=\frac{2\sqrt3}{3}$

$2)\; x=\sqrt[3]{\sqrt5+2}-\sqrt[3]{\sqrt5-2}\\\\(a-b)^3=a^3-b^3-3ab(a-b)\\\\x^3=(\sqrt5+2)-(\sqrt5-2)-3\sqrt[3]{(\sqrt5+2)(\sqrt5-2)}\cdot \\\\ \cdot (\sqrt[3]{ \sqrt5+2}-\sqrt[3]{\sqrt5+2})=4-3\sqrt[3]{5-4}(\sqrt[3]{\sqrt5-2}-\sqrt[3]{\sqrt5+2})=\\\\=4-3(\sqrt[3]{\sqrt5-2}-\sqrt[3]{\sqrt5+2})\\\\x^3+3x=4-3(\sqrt[3]{\sqrt5-2}-\sqrt[3]{\sqrt5+2})+3(\sqrt[3]{\sqrt5-2}-\sqrt[3]{\sqrt5+2})=4$.

Тук11 26 июл. 2018 г., 18:37:31 | 5 - 9 классы

Решите, пожалуйста Решить системы уравнений Картинка прилагается?

Решите, пожалуйста Решить системы уравнений Картинка прилагается.

Ingwar01 23 авг. 2018 г., 00:23:09 | 5 - 9 классы

Решите, пожалуйста Решить тригонометрические уравнения, картинка прилагается?

Решите, пожалуйста Решить тригонометрические уравнения, картинка прилагается.

Dashkasmerteeva 19 авг. 2018 г., 16:03:21 | 5 - 9 классы

Решите, пожалуйста Картинка прилагается?

Решите, пожалуйста Картинка прилагается.

Юля08 19 нояб. 2018 г., 23:51:45 | 5 - 9 классы

Решите, пожалуйста Решить системы уравнений Картинка прилагается?

Решите, пожалуйста Решить системы уравнений Картинка прилагается.

Кристинка11072003 29 авг. 2018 г., 22:17:53 | 5 - 9 классы

Решите, пожалуйста Решить тригонометрические уравнения, картинка прилагается?

Решите, пожалуйста Решить тригонометрические уравнения, картинка прилагается.

Алина789456 20 авг. 2018 г., 16:45:01 | 5 - 9 классы

Решите, пожалуйста Надо решить уравнение Картинка прилагается?

Решите, пожалуйста Надо решить уравнение Картинка прилагается.

Kristivip 10 июл. 2018 г., 19:16:29 | 5 - 9 классы

Решите, пожалуйста Решить тригонометрические уравнения, картинка прилагается?

Решите, пожалуйста Решить тригонометрические уравнения, картинка прилагается.

Sveta2001r 20 июн. 2018 г., 22:33:02 | 5 - 9 классы

Решите, пожалуйста Решить тригонометрические уравнения, картинка прилагается?

Решите, пожалуйста Решить тригонометрические уравнения, картинка прилагается.

Хдхдхд1 31 авг. 2018 г., 14:52:53 | 5 - 9 классы

Решите, пожалуйста Решить системы уравнений Картинка прилагается?

Решите, пожалуйста Решить системы уравнений Картинка прилагается.

Happywolf8 19 сент. 2018 г., 13:36:19 | 5 - 9 классы

Решите, пожалуйста Решить тригонометрические уравнения, картинка прилагается?

Решите, пожалуйста Решить тригонометрические уравнения, картинка прилагается.